题目内容
已知{an}是公差不为零的等差数列,a1=1,且a1,a3,a9成等比数列.
(1)求数列{an}的通项公式;(2)求数列{an}的前n项和Sn.
解:(1)由题设知公差d≠0,由a1=1,a1,a3,a9成等比数列,
得(1+2d)2=1×(1+8d),即d2-d=0,…(4分)
解得d=1,d=0(舍去),…(6分)
故{an}的通项an=1+(n-1)×1=n.…(9分)
(2)由(Ⅰ)及等差数列前n项和公式得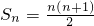 …(14分)
…(14分)
分析:(1)设出公差d,由a1,a3,a9成等比数列得关于d的一元二次方程,解得d=1,d=0,{an}是公差不为零的等差数列,d=1,再由a1=1,代入通项公式可求解;
(2)由(1)知,d=1,又已知a1=1,{an}是等差数列,选择含有首项a1和公差d等差数列的前n项和公式代入即可.
点评:本题主要考查等差数列的通项公式及前n项和公式,已知数列为等差数列,求通项公式,求首项和公差即可;求前n项和时,有两个公式,结合已知,选择一个最易计算的公式.
得(1+2d)2=1×(1+8d),即d2-d=0,…(4分)
解得d=1,d=0(舍去),…(6分)
故{an}的通项an=1+(n-1)×1=n.…(9分)
(2)由(Ⅰ)及等差数列前n项和公式得
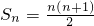 …(14分)
…(14分)分析:(1)设出公差d,由a1,a3,a9成等比数列得关于d的一元二次方程,解得d=1,d=0,{an}是公差不为零的等差数列,d=1,再由a1=1,代入通项公式可求解;
(2)由(1)知,d=1,又已知a1=1,{an}是等差数列,选择含有首项a1和公差d等差数列的前n项和公式代入即可.
点评:本题主要考查等差数列的通项公式及前n项和公式,已知数列为等差数列,求通项公式,求首项和公差即可;求前n项和时,有两个公式,结合已知,选择一个最易计算的公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目