题目内容
已知 ,设
,设 ,则在y轴右侧由函数f(x)的图象与x轴、直线x=e所围成的封闭图形的面积为 .
,则在y轴右侧由函数f(x)的图象与x轴、直线x=e所围成的封闭图形的面积为 .
【答案】分析:由新定义求出函数的解析式,根据解析式画出x>0时的图象,再利用定积分求出面积即可.
解答:解:令 .
.
当x>1或-1<x<0时,h(x)>0;当x≤-1或0<x≤1时,h(x)≤0.
∴ ,
,
当x>0时,画出函数的图象为:
则在y轴右侧由函数f(x)的图象与x轴、直线x=e所围成的封闭图形的面积= +
+ =
= +
+ =
= .
.
故答案为 .
.
点评:由新定义求出函数的解析式是求面积的前提,利用定积分求面积是求面积的通法,应熟练掌握.
解答:解:令
 .
.当x>1或-1<x<0时,h(x)>0;当x≤-1或0<x≤1时,h(x)≤0.

∴
 ,
,当x>0时,画出函数的图象为:
则在y轴右侧由函数f(x)的图象与x轴、直线x=e所围成的封闭图形的面积=
 +
+ =
= +
+ =
= .
.故答案为
 .
.点评:由新定义求出函数的解析式是求面积的前提,利用定积分求面积是求面积的通法,应熟练掌握.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目

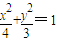 的右焦点为F,左顶点为A,点P为曲线D上的动点,以PF为直径的圆恒与y轴相切.
的右焦点为F,左顶点为A,点P为曲线D上的动点,以PF为直径的圆恒与y轴相切.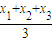 ,
, ))
))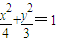 的右焦点为F,左顶点为A,点P为曲线D上的动点,以PF为直径的圆恒与y轴相切.
的右焦点为F,左顶点为A,点P为曲线D上的动点,以PF为直径的圆恒与y轴相切.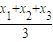 ,
,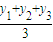 ))
))