Question

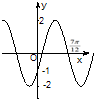已知函数f（x）=2sin（ωx+φ）（ω＞0，|φ|＜π）的部分图象如图所示，那么f（x）的表达式为（　　）

• A、f(x)=2sin(2x+

  5π

  6

  )
• B、f(x)=2sin(2x-

  5π

  6

  )
• C、f(x)=2sin(2x+

  π

  6

  )
• D、f(x)=2sin(2x-

  π

  6

  )

Answer 1

分析：由f（x）的图象过点（0，1），得f（0）=-1，结合φ的范围可求φ值，由f（x）的图象过点（

7π

12

，0）及“五点法”作图可得ω×

7π

12

-

π

6

=π．

解答：解：由图象可知f（x）的图象过点（0，1），
∴f（0）=-1，即2sinφ=-1，
又|φ|＜π，
∴φ=-

π

6

，
又∵f（x）的图象过点（

7π

12

，0），
∴ω×

7π

12

-

π

6

=π，解得ω=2，
∴f（x）=2sin（2x-

π

6

），
故选D．

点评：本题考查y=Asin（ωx+φ）的图象变换，考查数形结合思想，考查学生解决问题的能力．