题目内容
点M(a,b)是圆x2+y2=r2内异于圆心的一点,则直线ax+by-r2=0与圆的交点的个数是( )
| A、1 | B、2 | C、0 | D、需讨论确定 |
分析:首先由点M在圆x2+y2=r2的内部且异于圆心,得出a、b、r间的关系式0<a2+b2<r2,即0<
<r;
然后求出圆心(0,0)到直线ax+by-r2=0的距离d=
;此时结合条件可比较得出d与半径r的大小关系d>r,
则直线与圆无交点.
| a2+b2 |
然后求出圆心(0,0)到直线ax+by-r2=0的距离d=
| r2 | ||
|
则直线与圆无交点.
解答:解:因为点M(a,b)是圆x2+y2=r2内异于圆心的一点,
所以0<a2+b2<r2,所以0<
<r,
则圆心(0,0)到直线ax+by-r2=0的距离d=
>r,
所以直线ax+by-r2=0与圆x2+y2=r2无交点.
故选C.
所以0<a2+b2<r2,所以0<
| a2+b2 |
则圆心(0,0)到直线ax+by-r2=0的距离d=
| r2 | ||
|
所以直线ax+by-r2=0与圆x2+y2=r2无交点.
故选C.
点评:本题主要考查点与圆的位置关系及直线与圆的位置关系.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目


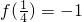 ; ②f(x)的图象关于
; ②f(x)的图象关于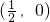 对称; ③若
对称; ③若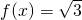 ,则
,则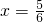 ; ④f(x)在(0,1)上单调递增.
; ④f(x)在(0,1)上单调递增.
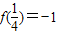 ; ②f(x)的图象关于
; ②f(x)的图象关于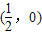 对称; ③若
对称; ③若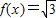 ,则
,则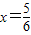 ; ④f(x)在(0,1)上单调递增.
; ④f(x)在(0,1)上单调递增.
 ; ②f(x)的图象关于
; ②f(x)的图象关于 对称; ③若
对称; ③若 ,则
,则 ; ④f(x)在(0,1)上单调递增.
; ④f(x)在(0,1)上单调递增.