题目内容
已知数列{an}满足an+1=|an-1|(n∈N*),
(1)若 ,求an;
,求an;
(2)是否存在a1,n0(a1∈R,n0∈N*),使当n≥n0(n∈N*)时,an恒为常数。若存在,求a1,n0,否则说明理由;
(3)若a1=a∈(k,k+1)(k∈N*),求{an}的前3k项的和S3k(用k,a表示)。
(1)若
 ,求an;
,求an;(2)是否存在a1,n0(a1∈R,n0∈N*),使当n≥n0(n∈N*)时,an恒为常数。若存在,求a1,n0,否则说明理由;
(3)若a1=a∈(k,k+1)(k∈N*),求{an}的前3k项的和S3k(用k,a表示)。
解:(1)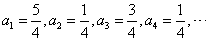 ,
,
∴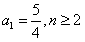 时,
时,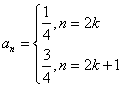 ,其中k∈N*。
,其中k∈N*。
(2)因为存在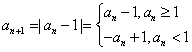 ,
,
所以,当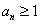 时,
时,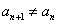 ,
,
①若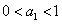 ,则
,则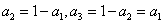 ,此时只需:
,此时只需: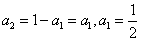 ,
,
故存在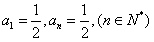 ;
;
②若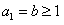 ,不妨设
,不妨设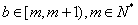 ,易知,
,易知,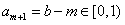 ,
,
∴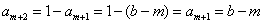 ,
,
∴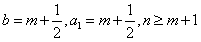 时,
时,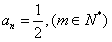 ;
;
③若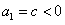 ,不妨设
,不妨设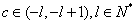 ,易知
,易知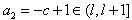 ,
,
∴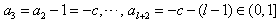 ,
,
∴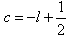 ,∴
,∴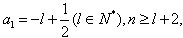 则
则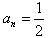 ,
,
故存在三组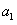 和
和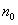 :
: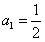 时,
时,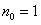 ;
;
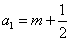 时,
时,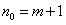 ;
;
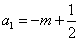 时,
时,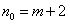 ,其中
,其中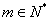 。
。
(3)当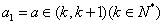 时,
时,
易知,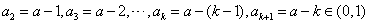 ,
,
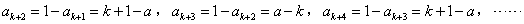 ,
,
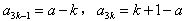 ,
,
∴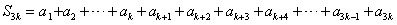
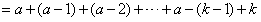
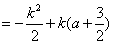 。
。
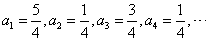 ,
,∴
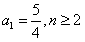 时,
时,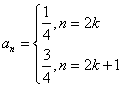 ,其中k∈N*。
,其中k∈N*。(2)因为存在
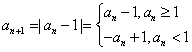 ,
,所以,当
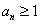 时,
时,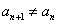 ,
,①若
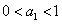 ,则
,则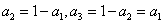 ,此时只需:
,此时只需: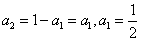 ,
,故存在
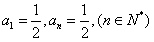 ;
;②若
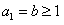 ,不妨设
,不妨设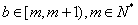 ,易知,
,易知,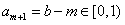 ,
,∴
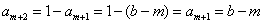 ,
,∴
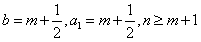 时,
时,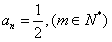 ;
;③若
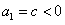 ,不妨设
,不妨设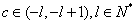 ,易知
,易知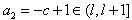 ,
,∴
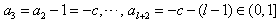 ,
,∴
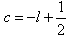 ,∴
,∴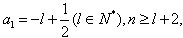 则
则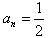 ,
,故存在三组
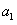 和
和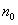 :
: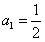 时,
时,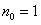 ;
;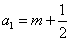 时,
时,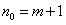 ;
;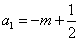 时,
时,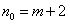 ,其中
,其中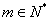 。
。(3)当
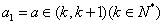 时,
时,易知,
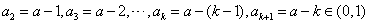 ,
,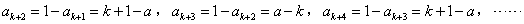 ,
,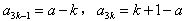 ,
, ∴
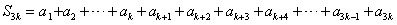
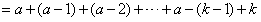
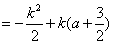 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目