题目内容
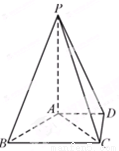
如图,在四棱锥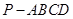 中,
中,  平面
平面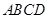 ,
, ,
,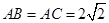 ,
, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求棱锥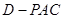 的高.
的高.
【答案】
(1)证明见试题解析;(2)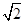 .
.
【解析】
试题分析:(1)要证明线面垂直,需要找出平面中两条相交直线,易知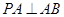 ,根据数量关系,利用勾股定理能够知道
,根据数量关系,利用勾股定理能够知道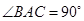 ,即
,即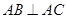 ,从而就能够证出
,从而就能够证出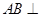 平面
平面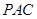 ;(2)解答本题有两种方法.方法一:直接作出高.由
;(2)解答本题有两种方法.方法一:直接作出高.由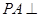 平面
平面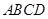 知平面
知平面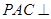 平面
平面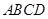 ,在
,在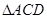 中,过D作
中,过D作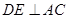 于
于 则
则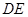 为三棱锥
为三棱锥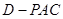 的高,进而求出
的高,进而求出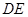 的长.方法二:三棱锥等体积法.根据
的长.方法二:三棱锥等体积法.根据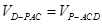 ,则
,则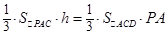 ,从而求出
,从而求出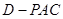 的高
的高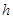 .
.
试题解析:(1)证明: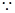
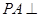 平面
平面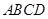
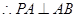
在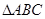 中,
中,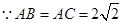 ,
,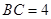
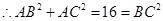
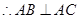
又
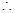
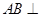 平面
平面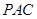
(2)

方法一:作出三棱锥的高
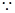
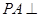 平面
平面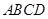 ,
,
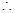 平面
平面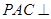 平面
平面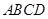
 在
在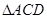 中,过D作
中,过D作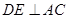 于
于 ,则
,则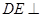 平面
平面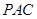
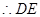 为三棱锥
为三棱锥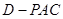 的高
的高
又 在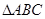 中,过
中,过 作
作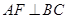 于
于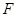 ,则
,则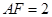
 在
在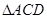 中,
中, 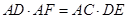
即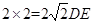 ,
,
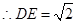
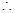 三棱锥
三棱锥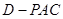 的高为
的高为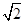
方法二:等体积变换法
在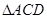 中,过
中,过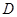 作
作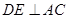 于
于 ,
,
在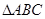 中,
过
中,
过 作
作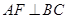 于
于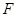 ,则
,则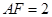
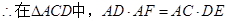
即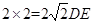 ,
,
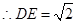
又设三棱锥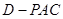 的高为
的高为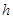 ,
,
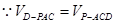 ,
,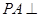 平面
平面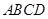
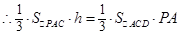 即
即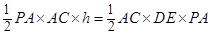
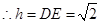
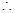 三棱锥
三棱锥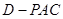 的高为
的高为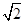
考点:立体几何线面垂直的证明,三棱锥的体积及高的求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在四棱锥
如图,在四棱锥
 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD, ,E是PC的中点.
,E是PC的中点.
 平面EDB;
平面EDB; 中,底面
中,底面 为菱形,
为菱形, ,
,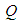 为
为 的中点。
的中点。
 ,求证:平面
,求证:平面 ;
; 在线段
在线段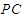 上,
上, ,试确定
,试确定 的值,使
的值,使 ;
; 中,底面
中,底面 为直角梯形,
为直角梯形, ,
, ,平面
,平面 ⊥底面
⊥底面 为AD的中点,
为AD的中点, 是棱
是棱 上的点,
上的点, ,
, .(1)若
.(1)若
 ;(2)求证:平面
;(2)求证:平面 ⊥平面
⊥平面