题目内容
已知数列{an}满足a1=2,前n项和为Sn,an+1=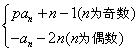 ,
,
(1)若数列{bn}满足bn=a2n+a2n+1(n≥1),试求数列{bn}前3项的和T3;
(2)(理)若数列{cn}满足cn=a2n,试判断{cn}是否为等比数列,并说明理由;
(文)若数列满足cn=a2n,p=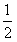 ,求证:{cn}是为等比数列;
,求证:{cn}是为等比数列;
(3)当p=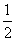 时,对任意n∈N*,不等式S2n+1≤
时,对任意n∈N*,不等式S2n+1≤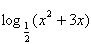 都成立,求x的取值范围。
都成立,求x的取值范围。
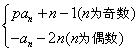 ,
,(1)若数列{bn}满足bn=a2n+a2n+1(n≥1),试求数列{bn}前3项的和T3;
(2)(理)若数列{cn}满足cn=a2n,试判断{cn}是否为等比数列,并说明理由;
(文)若数列满足cn=a2n,p=
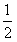 ,求证:{cn}是为等比数列;
,求证:{cn}是为等比数列; (3)当p=
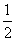 时,对任意n∈N*,不等式S2n+1≤
时,对任意n∈N*,不等式S2n+1≤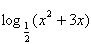 都成立,求x的取值范围。
都成立,求x的取值范围。 解:(1)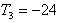 ;
;
(2)(理)当p=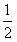 时,数列{cn}成等比数列;
时,数列{cn}成等比数列;
当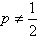 时,数列{cn}不为等比数列;
时,数列{cn}不为等比数列;
理由如下:因为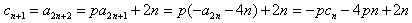 ,
,
所以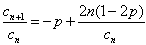 ,
,
故当p=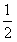 时,数列{cn}是首项为1,公比为
时,数列{cn}是首项为1,公比为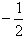 的等比数列;
的等比数列;
当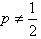 时,数列{cn}不成等比数列。
时,数列{cn}不成等比数列。
(文)因为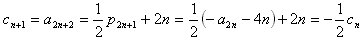 ,
,
所以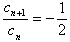 ,
,
故当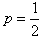 时,数列{cn}是首项为1,公比为
时,数列{cn}是首项为1,公比为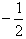 的等比数列;
的等比数列;
(3)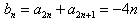 ,
,
所以{bn}成等差数列;
当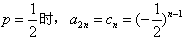 ,
,
因为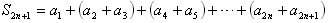 ,
,
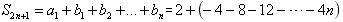
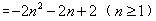 ,
,
又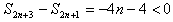 ,
,
所以{S2n+1}单调递减,
当n=1时,S3最大为-2,
所以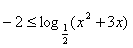 ,
,
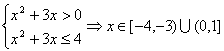 。
。
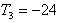 ;
;(2)(理)当p=
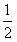 时,数列{cn}成等比数列;
时,数列{cn}成等比数列; 当
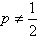 时,数列{cn}不为等比数列;
时,数列{cn}不为等比数列;理由如下:因为
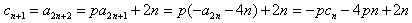 ,
,所以
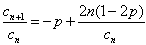 ,
,故当p=
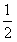 时,数列{cn}是首项为1,公比为
时,数列{cn}是首项为1,公比为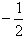 的等比数列;
的等比数列; 当
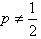 时,数列{cn}不成等比数列。
时,数列{cn}不成等比数列。(文)因为
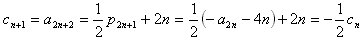 ,
,所以
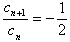 ,
,故当
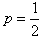 时,数列{cn}是首项为1,公比为
时,数列{cn}是首项为1,公比为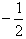 的等比数列;
的等比数列; (3)
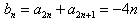 ,
,所以{bn}成等差数列;
当
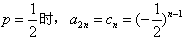 ,
,因为
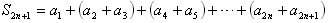 ,
,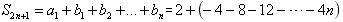
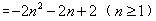 ,
,又
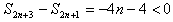 ,
,所以{S2n+1}单调递减,
当n=1时,S3最大为-2,
所以
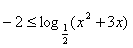 ,
,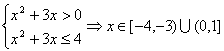 。
。
练习册系列答案
相关题目