题目内容
已知数列{an} 的通项公式an=3n-26,前n项和为Sn,则当Sn最小时,n=________.
8
分析:由an=3n-26,可知数列{an} 是首项为-23,公差为3的单调递增的等差数列,由其所有非正数项之和最小即可得到答案.
解答:∵an=3n-26,是n的一次函数,
∴数列{an} 是首项为-23,公差为3的单调递增的等差数列,
由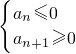 得:
得:
解得: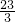 ≤n≤
≤n≤ ,又n∈Z,
,又n∈Z,
∴n=8.
故答案为:8.
点评:本题考查等差数列的前n项和,可以通过求和公式配方解决,也可以如上从通项入手解决,属于中档题.
分析:由an=3n-26,可知数列{an} 是首项为-23,公差为3的单调递增的等差数列,由其所有非正数项之和最小即可得到答案.
解答:∵an=3n-26,是n的一次函数,
∴数列{an} 是首项为-23,公差为3的单调递增的等差数列,
由
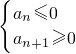 得:
得:
解得:
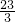 ≤n≤
≤n≤ ,又n∈Z,
,又n∈Z,∴n=8.
故答案为:8.
点评:本题考查等差数列的前n项和,可以通过求和公式配方解决,也可以如上从通项入手解决,属于中档题.

练习册系列答案
相关题目