题目内容
6名同学从左到右站成一排,其中甲不能站在两头,不同的站法有( )种
| A.480 | B.240 | C.120 | D.96 |
A
解析试题分析:先排甲同学有 种不同的方法,再排其余同学有
种不同的方法,再排其余同学有 种不同的方法,根据分步原理可知,共有4×120=480种不同的站法,故选A
种不同的方法,根据分步原理可知,共有4×120=480种不同的站法,故选A
考点:本题考查了排列组合的运用
点评:对于特殊元素的排列问题,往往利用特殊元素优先安排或者特殊位置优先安排的原则处理

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的展开式中含
的展开式中含 的正整数指数幂的项数是( )
的正整数指数幂的项数是( )
| A.0 | B.2 | C.4 | D.6 |
设函数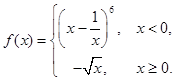 ,则当x>0时,
,则当x>0时, 表达式的展开式中常数项为
表达式的展开式中常数项为
| A.-20 | B.20 | C.-15 | D.15 |
 年第
年第 届全国运动会将在沈阳举行,某校
届全国运动会将在沈阳举行,某校 名大学生申请当
名大学生申请当 三个比赛项目的志愿者,组委会接受了他们的申请,每个比赛项目至少分配一人,每人只能服务一个比赛项目,若甲要求不去服务
三个比赛项目的志愿者,组委会接受了他们的申请,每个比赛项目至少分配一人,每人只能服务一个比赛项目,若甲要求不去服务 比赛项目,则不同的安排方案共有
比赛项目,则不同的安排方案共有
A. 种 种 | B. 种 种 | C.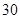 种 种 | D. 种 种 |
现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张.从中任取3张,要求这3张卡片不能是同一种颜色,且红色卡片至多1张.不同取法的种数为 ( )
| A.232 | B.252 | C.472 | D.484 |
若x为自然数,且 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
甲、乙等5人站成一排,其中甲、乙不相邻的不同排法共有( )
| A.144种 | B.72种 | C.36 种 | D.12种 |

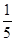
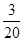

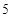 架舰载机准备着舰,如果甲、乙两机必须相邻着舰,而丙、丁两机不能相邻着舰,那么不同的着舰方法有( )
架舰载机准备着舰,如果甲、乙两机必须相邻着舰,而丙、丁两机不能相邻着舰,那么不同的着舰方法有( )