题目内容
已知f(x)=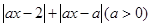 .
.
(1)当a=1时,求f(x)≥x的解集;
(2)若不存在实数x,使f(x)<3成立,求a的取值范围.
(1) ;(2)
;(2) 
解析试题分析:(1)根据绝对值的几何意义分类去掉绝对值符号,化为几个整式不等式,然后求解,最后求它们的并集即可.
(2)由题意可知 恒成立,由绝对值不等式的性质可得
恒成立,由绝对值不等式的性质可得 ,即
,即 ,解出a即可.
,解出a即可.
试题解析:(1)当a=1时,
 ,解得
,解得 ;
;
当 时,解得
时,解得 ,
, 无解
无解 ,解得
,解得 ; 3分
; 3分
综上可得到解集 . 5分
. 5分
(2)依题意,  ,
,
则 , 8分
, 8分
 (舍),
(舍),
所以 10分
10分
考点:解绝对值不等式的解法.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
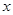 的不等式
的不等式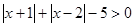 .
.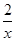 .
.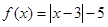 ,
,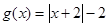 。
。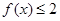 的解集;
的解集;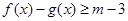 有解,求实数
有解,求实数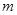 的取值范围。
的取值范围。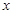 的一元二次不等式
的一元二次不等式 .
.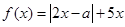 ,其中实数
,其中实数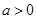 .
.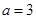 时,求不等式
时,求不等式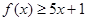 的解集;
的解集;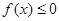 的解集为
的解集为 ,求
,求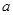 的值.
的值.