题目内容
如图,有长20m的铁丝网,若一边靠墙围成3个大小相同,紧紧相接的长方形,问每个小长方形的长和宽各是多少时,三个长方形的总面积最大?并求最大面积.


设每个小长方形的长和宽分别为x,y
则3x+4y=20,y=
(20-3x)
∴三个长方形的总面积:
S=3xy=3x×
(20-3x)
∴S=-
x2+15x
=-
(x2-
x)
=-
(x-
)2+25
又∵x>0,y=
(20-3x)>0
∴0<x<
∴x=
时,Smax=25,
此时y=
答:每个小长方形的长和宽分别为
,
时,三个长方形的总面积最大为25
则3x+4y=20,y=
| 1 |
| 4 |
∴三个长方形的总面积:
S=3xy=3x×
| 1 |
| 4 |
∴S=-
| 9 |
| 4 |
=-
| 9 |
| 4 |
| 20 |
| 3 |
=-
| 9 |
| 4 |
| 10 |
| 3 |
又∵x>0,y=
| 1 |
| 4 |
∴0<x<
| 20 |
| 3 |
∴x=
| 10 |
| 3 |
此时y=
| 5 |
| 2 |
答:每个小长方形的长和宽分别为
| 10 |
| 3 |
| 5 |
| 2 |

练习册系列答案
相关题目
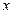 年后若人均一年占有
年后若人均一年占有 千克粮食,求出函数
千克粮食,求出函数 为常数,其中
为常数,其中 的图象如右图,则下列结论成立的是( )
的图象如右图,则下列结论成立的是( )



