题目内容
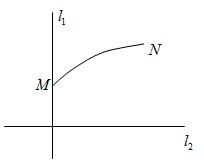
如图,l1、l2是通过某市开发区中心O的南北和东西走向的两条道路,连接M、N两地的铁路是一段抛物线弧,它所在的抛物线关于直线l1对称.M到l1、l2的距离分别是2 km、4 km,N到l1、l2的距离分别是3 km、9 km.
(1)建立适当的坐标系,求抛物线弧MN的方程;
 (2)该市拟在点O的正北方向建设一座工厂,考虑到环境问题,要求厂址到点O的距离大于5 km而不超过8 km,并且铁路上任意一点到工厂的距离不能小于
(2)该市拟在点O的正北方向建设一座工厂,考虑到环境问题,要求厂址到点O的距离大于5 km而不超过8 km,并且铁路上任意一点到工厂的距离不能小于![]() km,求该厂离点O的最近距离.(注:工厂视为一个点)
km,求该厂离点O的最近距离.(注:工厂视为一个点)
解:

(1)分别以l2、l1为x轴、y轴建立如图所示的平面直角坐标系,
则M(2,4),N(3,9).
设MN所在抛物线的方程为y=ax2+c,则有![]() 解得
解得![]()
故所求抛物线弧MN的方程为
y=x2(2≤x≤3).
(2)设抛物线弧上任意一点P(x,x2)(2≤x≤3),
厂址为点A(0,t)(5<t≤8).
 ∴t的最小值为
∴t的最小值为![]() .
.
所以,该厂距离点O的最近距离为6.25 km.

练习册系列答案
相关题目
 如图,l1、l2是通过某城市开发区中心O的两条南北和东西走向的街道,连接M、N两地之间的铁路线是圆心在l2上的一段圆弧.若点M在点O正北方向,且|MO|=3km,点N到l1、l2的距离分别为4km和5km.
如图,l1、l2是通过某城市开发区中心O的两条南北和东西走向的街道,连接M、N两地之间的铁路线是圆心在l2上的一段圆弧.若点M在点O正北方向,且|MO|=3km,点N到l1、l2的距离分别为4km和5km. ,求该校址距点O的最近距离(注:校址视为一个点).
,求该校址距点O的最近距离(注:校址视为一个点).
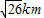 ,求该校址距点O的最近距离(注:校址视为一个点).
,求该校址距点O的最近距离(注:校址视为一个点).
 ,求该校址距点O的最近距离(注:校址视为一个点).
,求该校址距点O的最近距离(注:校址视为一个点).
 ,求该校址距点O的最近距离(注:校址视为一个点).
,求该校址距点O的最近距离(注:校址视为一个点).