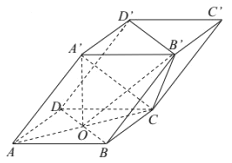
题目内容
【题目】如图,四棱柱![]() 的底面
的底面![]() 是菱形,
是菱形, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,直线
,直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .若存在,求
.若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)用几何法证明,先证得![]() 平面
平面![]() ,再证平面
,再证平面![]() 平面
平面![]() .
.
(Ⅱ)由条件可得![]() 两两相互垂直,故可建立坐标系,转化为代数运算求解。
两两相互垂直,故可建立坐标系,转化为代数运算求解。
试题解析:(Ⅰ)证明:
因为![]() ,
, ![]() 为
为![]() 的中点,
的中点,
则![]() .
.
又因为四边形![]() 是菱形,
是菱形,
所以![]() ,
,
因为![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(Ⅱ)在菱形![]() 中,由
中,由![]() ,可得
,可得![]() ,
, ![]()
由![]() ,可得
,可得![]() .
.
在三角形![]() 中,由
中,由![]() ,可得
,可得![]() .
.
故得![]() 两两相互垂直.
两两相互垂直.
以![]() 为原点,
为原点, ![]() 方向为
方向为![]() 轴正方向建立如图所示空间直角坐标系.
轴正方向建立如图所示空间直角坐标系.
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
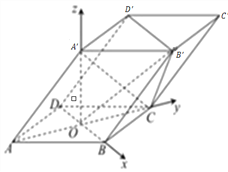
由![]() ,可得
,可得![]() ,
, ![]() ,
,
设![]() ,
, ![]() ,
,
所以![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
因为![]() ,
, ![]() ,
,
所以由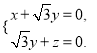 得
得![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,由题意得
,由题意得
![]()
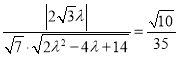
解得 ![]() 或
或![]() .
.
当![]() 时,
时, ![]() ; 当
; 当![]() 时,
时, ![]()
所以![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】为了弘扬民族文化,某校举行了“我爱国学,传诵经典”考试,并从中随机抽取了100名考生的成绩(得分均为整数,满足100分)进行统计制表,其中成绩不低于80分的考生被评为优秀生,请根据频率分布表中所提供的数据,用频率估计概率,回答下列问题.
分组 | 频数 | 频率 |
| 5 | 0.05 |
|
| 0.20 |
| 35 |
|
| 25 | 0.25 |
| 15 | 0.15 |
合计 | 100 | 1.00 |
(1)求![]() 的值并估计这100名考生成绩的平均分;
的值并估计这100名考生成绩的平均分;
(2)按频率分布表中的成绩分组,采用分层抽样抽取20人参加学校的“我爱国学”宣传活动,求其中优秀生的人数;