Question

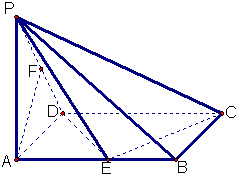
在四棱锥P－ABCD中，∠ABC＝∠ACD＝90°，∠BAC＝∠CAD＝60°，PA⊥平面ABCD，E为PD的中点，PA＝2AB＝2．

（Ⅰ）求四棱锥P－ABCD的体积V；

（Ⅱ）若F为PC的中点，求证PC⊥平面AEF；

 

 

Answer 1

【答案】

  （Ⅰ）V＝． （Ⅱ）见解析

【解析】(I)解本小题的关键是求底ABCD的面积.利用求解即可.

(II)证明线面垂直根据判定定理关键是证直线垂直这个平面内的两条相交直线.本小题可以证明：AF⊥PC, EF⊥PC即可

（Ⅰ）在Rt△ABC中，AB＝1，

∠BAC＝60°，∴BC＝，AC＝2．

在Rt△ACD中，AC＝2，∠CAD＝60°，

∴CD＝2，AD＝4．

∴S_ABCD＝

．……………… 3分

则V＝．     ……………… 5分

（Ⅱ）∵PA＝CA，F为PC的中点，

∴AF⊥PC．            ……………… 7分

∵PA⊥平面ABCD，∴PA⊥CD．

∵AC⊥CD，PA∩AC＝A，

∴CD⊥平面PAC．∴CD⊥PC．

∵E为PD中点，F为PC中点，

∴EF∥CD．则EF⊥PC．       ……… 11分

∵AF∩EF＝F，∴PC⊥平面AEF．