题目内容
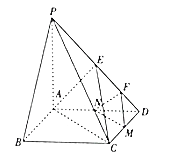
【题目】在如图所示的四棱锥![]() 中,四边形
中,四边形![]() 为正方形,
为正方形, ![]() 平面
平面![]() ,且
,且![]() 分别为
分别为![]() 的中点,
的中点, ![]() .
.
证明:(1)![]() 平面
平面![]() ;
;
若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析(2) ![]()
【解析】试题分析:(1)连结![]() ,分别交
,分别交![]() 于点
于点![]() ,连结
,连结![]() ,推导出
,推导出![]() ,
, ![]() ,
, ![]() ,由此能证明
,由此能证明![]() 平面
平面![]() ;(2)以
;(2)以![]() 为坐标原点,
为坐标原点, ![]() ,
, ![]() ,
, ![]() 所在直线分别为
所在直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立空间直角坐标系,利用向量法能求出二面角
轴建立空间直角坐标系,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
试题解析:(1)证明: 连结![]() ,分别的交
,分别的交![]() 于点
于点![]() ,连结
,连结![]()
![]() 为
为![]() 中点,
中点, ![]() 为
为![]() 中点,
中点, ![]() .又
.又![]() 为
为![]() 中点,
中点,
又![]() 为
为![]() 的中点,
的中点, ![]()
![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() .
.
(2)![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() .
.
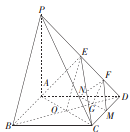
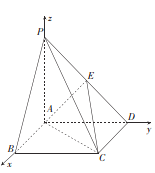
如图,以![]() 为坐标原点,
为坐标原点, ![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴轴建立空间直角坐标系,
轴轴建立空间直角坐标系,
则![]() ,则
,则![]()
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 的一个法向量
的一个法向量![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,
则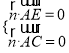 ,即
,即![]() ,
,
令![]() ,则
,则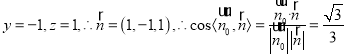 ,
,
由图可知,二面角![]() 为饨角,
为饨角, ![]() 二面角
二面角![]() 的余弦值
的余弦值![]() .
.

练习册系列答案
相关题目
【题目】为做好2022年北京冬季奥运会的宣传工作,组委会计划从某大学选取若干大学生志愿者,某记者在该大学随机调查了1000名大学生,以了解他们是否愿意做志愿者工作,得到的数据如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合计 | |
男大学生 | 610 | ||
女大学生 | 90 | ||
合计 | 800 |
(1) 根据题意完成表格;
(2) 是否有![]() 的把握认为愿意做志愿者工作与性别有关?
的把握认为愿意做志愿者工作与性别有关?
参考公式及数据: 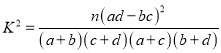 ,其中
,其中![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【题目】学校射击队的某一选手射击一次,其命中环数的概率如表:
命中环数 | 10环 | 9环 | 8环 | 7环 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求该选手射击一次,
(1)命中9环或10环的概率.
(2)至少命中8环的概率.
(3)命中不足8环的概率.