题目内容
已知圆M经过点
，并且与直线
相切，圆心M的轨迹为曲线w．
（1）求w的方程
（2）若过点
的直线l与曲线w交与PQ两点，PQ中点的横坐标为
，求线段 PQ的长度．
，并且与直线相切，圆心M的轨迹为曲线w．（1）求w的方程
（2）若过点
的直线l与曲线w交与PQ两点，PQ中点的横坐标为，求线段 PQ的长度．解：（1）过点M作MN垂直直线线
于N．
依题意得|MN|=|AM|
所以动点M的轨迹为是以A（
，0）为焦点，直线x=﹣
为准线的抛物线，
即曲线w的方程是y2=6x
（2）依题意，直线l1，l2的斜率存在且不为0，
设直线l的方程为x=ky+
，化简得y2﹣6ky﹣9=0
设P（x1，y1），Q（x2，y2），则
x1+x2=5
∴|PQ|=|PA|+|AQ|=
+x2
=x1+x2+3=8
于N．依题意得|MN|=|AM|
所以动点M的轨迹为是以A（
，0）为焦点，直线x=﹣为准线的抛物线，即曲线w的方程是y2=6x
（2）依题意，直线l1，l2的斜率存在且不为0，
设直线l的方程为x=ky+
，化简得y2﹣6ky﹣9=0设P（x1，y1），Q（x2，y2），则
x1+x2=5
∴|PQ|=|PA|+|AQ|=
+x2=x1+x2+3=8
练习册系列答案
相关题目
，并且与直线
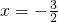相切，圆心M的轨迹为曲线w．
，求线段 PQ的长度．
，并且与直线
相切，圆心M的轨迹为曲线w．
的直线l与曲线w交与PQ两点，PQ中点的横坐标为
，求线段 PQ的长度．