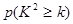题目内容
某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动,分别由李老师和张老师负责,已知该系共有 位学生,每次活动均需该系
位学生,每次活动均需该系 位学生参加(
位学生参加( 和
和 都是固定的正整数).假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系
都是固定的正整数).假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系 位学生,且所发信息都能收到.记该系收到李老师或张老师所发活动通知信息的学生人数为
位学生,且所发信息都能收到.记该系收到李老师或张老师所发活动通知信息的学生人数为
(Ⅰ)求该系学生甲收到李老师或张老师所发活动通知信息的概率;
(Ⅱ)求使 取得最大值的整数
取得最大值的整数 .
.
 位学生,每次活动均需该系
位学生,每次活动均需该系 位学生参加(
位学生参加( 和
和 都是固定的正整数).假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系
都是固定的正整数).假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系 位学生,且所发信息都能收到.记该系收到李老师或张老师所发活动通知信息的学生人数为
位学生,且所发信息都能收到.记该系收到李老师或张老师所发活动通知信息的学生人数为
(Ⅰ)求该系学生甲收到李老师或张老师所发活动通知信息的概率;
(Ⅱ)求使
 取得最大值的整数
取得最大值的整数 .
.(Ⅰ) (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
本题是概率压轴题,难度大,文字多,考生不一定能够有时间去读懂,不仅如此还考查到了分类讨论思想,难度更高一层,但细细想来,它也就那回事.第(1)题该系学生甲收到李老师或张老师所发活动通知信息要从反面角度去思考,没有收到信息的概率是什么,由于A和B是相互独立, ,没有收到信息的概率正好是
,没有收到信息的概率正好是 ,所以最后的结果就能求出;第(2)题考查的考点比较多,而且
,所以最后的结果就能求出;第(2)题考查的考点比较多,而且 和
和 都是变量,遇到变量就要做好讨论的准备,于是本题要从
都是变量,遇到变量就要做好讨论的准备,于是本题要从 和
和 两个角度考虑.当
两个角度考虑.当 时,
时, ,
, ;当
;当 时,整数
时,整数 满足
满足 ,其中
,其中 是
是 和
和 中的较小者,从而表示出
中的较小者,从而表示出 ,接着要根据题意找出不等关系:
,接着要根据题意找出不等关系: ,化简分离出
,化简分离出 ,而
,而 是否为整数,需要讨论,还需要考虑
是否为整数,需要讨论,还需要考虑 是否成立的问题,于是,接下来一方面需要讨论是否为整,另一方面要证明
是否成立的问题,于是,接下来一方面需要讨论是否为整,另一方面要证明 ,详细的解答如下.
,详细的解答如下.
设事件A:“学生甲收到李老师所发信息”,事件B:“学生甲收到张老师所发信息”,由题意A和B是相互独立的事件,则 与
与 相互独立,
相互独立,
而
所以
因此,学生甲收到活动通知信息的概率为
 .
.
当 时,
时, 只能取
只能取 ,有
,有
当 ,整数
,整数 满足
满足 ,其中
,其中 是
是 和
和 中的较小者.“李老师和张老师各自独立、随机地发活动通知信息给
中的较小者.“李老师和张老师各自独立、随机地发活动通知信息给 位同学”所包含的基本事件总数为
位同学”所包含的基本事件总数为 .
.
当 时,同时收到李老师和张老师转发信息的学生人数恰为
时,同时收到李老师和张老师转发信息的学生人数恰为 ,仅收到李老师或仅收到张老师转发信息的学生人数为
,仅收到李老师或仅收到张老师转发信息的学生人数为 ,则由乘法计数原理知:事件
,则由乘法计数原理知:事件 所含基本事件数为
所含基本事件数为
此时
当 ,
,

化简解得
假如 成立,
成立,
则当 能被
能被 整除时,
整除时,
 ,故
,故 在
在 和
和 处达到最大值;
处达到最大值;
则当 不能被
不能被 整除时,
整除时, 在
在 处达最大值.(注:
处达最大值.(注: 表示不超过
表示不超过 的最大整数).
的最大整数).
下证:
因为 ,所以
,所以 ,
,
 ,故
,故 ,显然
,显然 .
.
因此 .
.
【考点定位】考查古典概型,计数原理,分类讨论思想等基础知识.,以及运用数学知识分析和解决实际问题的能力.
 ,没有收到信息的概率正好是
,没有收到信息的概率正好是 ,所以最后的结果就能求出;第(2)题考查的考点比较多,而且
,所以最后的结果就能求出;第(2)题考查的考点比较多,而且 和
和 都是变量,遇到变量就要做好讨论的准备,于是本题要从
都是变量,遇到变量就要做好讨论的准备,于是本题要从 和
和 两个角度考虑.当
两个角度考虑.当 时,
时, ,
, ;当
;当 时,整数
时,整数 满足
满足 ,其中
,其中 是
是 和
和 中的较小者,从而表示出
中的较小者,从而表示出 ,接着要根据题意找出不等关系:
,接着要根据题意找出不等关系: ,化简分离出
,化简分离出 ,而
,而 是否为整数,需要讨论,还需要考虑
是否为整数,需要讨论,还需要考虑 是否成立的问题,于是,接下来一方面需要讨论是否为整,另一方面要证明
是否成立的问题,于是,接下来一方面需要讨论是否为整,另一方面要证明 ,详细的解答如下.
,详细的解答如下.设事件A:“学生甲收到李老师所发信息”,事件B:“学生甲收到张老师所发信息”,由题意A和B是相互独立的事件,则
 与
与 相互独立,
相互独立,而

所以

因此,学生甲收到活动通知信息的概率为
 .
.当
 时,
时, 只能取
只能取 ,有
,有
当
 ,整数
,整数 满足
满足 ,其中
,其中 是
是 和
和 中的较小者.“李老师和张老师各自独立、随机地发活动通知信息给
中的较小者.“李老师和张老师各自独立、随机地发活动通知信息给 位同学”所包含的基本事件总数为
位同学”所包含的基本事件总数为 .
.当
 时,同时收到李老师和张老师转发信息的学生人数恰为
时,同时收到李老师和张老师转发信息的学生人数恰为 ,仅收到李老师或仅收到张老师转发信息的学生人数为
,仅收到李老师或仅收到张老师转发信息的学生人数为 ,则由乘法计数原理知:事件
,则由乘法计数原理知:事件 所含基本事件数为
所含基本事件数为
此时

当
 ,
,

化简解得

假如
 成立,
成立,则当
 能被
能被 整除时,
整除时, ,故
,故 在
在 和
和 处达到最大值;
处达到最大值;则当
 不能被
不能被 整除时,
整除时, 在
在 处达最大值.(注:
处达最大值.(注: 表示不超过
表示不超过 的最大整数).
的最大整数).下证:

因为
 ,所以
,所以 ,
, ,故
,故 ,显然
,显然 .
.因此
 .
.【考点定位】考查古典概型,计数原理,分类讨论思想等基础知识.,以及运用数学知识分析和解决实际问题的能力.

练习册系列答案
相关题目
 22℃
22℃ ℃
℃

 列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.
列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.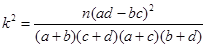







 ,求
,求