题目内容
如果椭圆 与双曲线
与双曲线 的焦点相同,则k的取值范围为( )
的焦点相同,则k的取值范围为( )A.2
B.k>3
C.k=2或k=4
D.0<k<2
【答案】分析:根据椭圆 与双曲线
与双曲线 的焦点相同,可分别求出椭圆和双曲线中的c2,让两者相等,就可得到关于k的方程,解方程即可得k值.
的焦点相同,可分别求出椭圆和双曲线中的c2,让两者相等,就可得到关于k的方程,解方程即可得k值.
解答:解:∵椭圆 与双曲线
与双曲线 的焦点相同,∴焦点在x轴上.
的焦点相同,∴焦点在x轴上.
∴在椭圆中,c2=9-k2,在双曲线中,c2=k+3
∴9-k2=k+3,k2+k-6=0
解得,k=2或-3
又∵k>0,∴k=2
故选A
点评:本题主要考查了椭圆和双曲线中a,b,c的关系,注意两者不要记混.
 与双曲线
与双曲线 的焦点相同,可分别求出椭圆和双曲线中的c2,让两者相等,就可得到关于k的方程,解方程即可得k值.
的焦点相同,可分别求出椭圆和双曲线中的c2,让两者相等,就可得到关于k的方程,解方程即可得k值.解答:解:∵椭圆
 与双曲线
与双曲线 的焦点相同,∴焦点在x轴上.
的焦点相同,∴焦点在x轴上.∴在椭圆中,c2=9-k2,在双曲线中,c2=k+3
∴9-k2=k+3,k2+k-6=0
解得,k=2或-3
又∵k>0,∴k=2
故选A
点评:本题主要考查了椭圆和双曲线中a,b,c的关系,注意两者不要记混.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
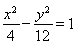
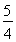
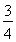
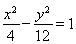
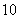
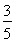
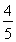
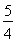
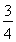
 与双曲线
与双曲线 的焦点相同,则k的取值范围为
的焦点相同,则k的取值范围为