题目内容
一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积是（ ）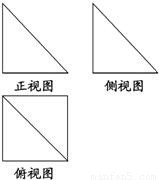
A．12π
B．4
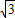πC．3π
D．12
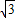π
【答案】分析：三视图复原几何体是四棱锥，扩展为正方体，它的体对角线，就是球的直径，求出半径，解出球的表面积．
解答：解：由三视图知该几何体为四棱锥，记作S-ABCD，
其中SA⊥面ABCD．面ABCD为正方形，将此四棱锥还原为正方体，易知正方体的体对角线即为外接球直径，所以2r=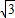
．
∴S球=4πr2=4π×
=3π．
答案：C
点评：本题考查三视图求表面积，几何体的外接球问题，是基础题．
解答：解：由三视图知该几何体为四棱锥，记作S-ABCD，
其中SA⊥面ABCD．面ABCD为正方形，将此四棱锥还原为正方体，易知正方体的体对角线即为外接球直径，所以2r=
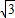．∴S球=4πr2=4π×
=3π．答案：C
点评：本题考查三视图求表面积，几何体的外接球问题，是基础题．
练习册系列答案
相关题目
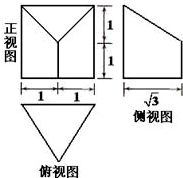
（2013•房山区二模）一个几何体的三视图如图所示，则这个几何体的表面积为（ ）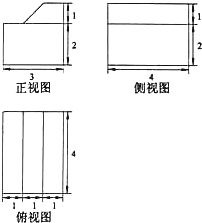
（2012•天津）一个几何体的三视图如图所示（单位：m），则该几何体的体积为
一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的表面积为
（2010•河东区一模）一个几何体的三视图如图所示，则该几何体（不考虑接触点）的表面积为