题目内容
下列命题中正确的是
- A.y=tanx为增函数
- B.y=sinx在第一象限为增函数
- C.
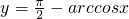 为奇函数
为奇函数 - D.y=sinx的反函数为y=arcsinx
C
分析:根据正切函数的定义域问题可排除A;根据第一象限的角的变化排除B;根据正弦函数的反函数的定义域问题排除D;根据奇函数的定义可验证C对.
解答:y=tanx应该是在每一个 上是增函数,排除A;
上是增函数,排除A;
y=sinx在(2kπ,2k )上是增函数,但在第一象限不是,排除B;
)上是增函数,但在第一象限不是,排除B;
y=sinx,x∈(- )的反函数为y=arcsinx,排除D
)的反函数为y=arcsinx,排除D
而 ,∴
,∴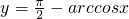 为奇函数
为奇函数
故选C
点评:本题主要考查三角函数的定义域问题.在三角函数中看单调性时一定要注意定义域,否则很容易出错.
分析:根据正切函数的定义域问题可排除A;根据第一象限的角的变化排除B;根据正弦函数的反函数的定义域问题排除D;根据奇函数的定义可验证C对.
解答:y=tanx应该是在每一个
 上是增函数,排除A;
上是增函数,排除A;y=sinx在(2kπ,2k
 )上是增函数,但在第一象限不是,排除B;
)上是增函数,但在第一象限不是,排除B;y=sinx,x∈(-
 )的反函数为y=arcsinx,排除D
)的反函数为y=arcsinx,排除D而
 ,∴
,∴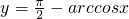 为奇函数
为奇函数故选C
点评:本题主要考查三角函数的定义域问题.在三角函数中看单调性时一定要注意定义域,否则很容易出错.

练习册系列答案
相关题目
 ,
, 及平面
及平面 ,
, ,下列命题中正确的是
,下列命题中正确的是 ,
, ,则
,则 ;
;  ,则
,则 ,
, ,则
,则 ;
;
 ,则
,则 .
. 唯一的一个零点同时在区间(0,16),(0,8),(0,4),(0,2)内,那么下列命题中正确的是(
).
唯一的一个零点同时在区间(0,16),(0,8),(0,4),(0,2)内,那么下列命题中正确的是(
).  则下列命题中正确的是
则下列命题中正确的是 的最小正周期为
的最小正周期为
 的最小值为
的最小值为
