题目内容
数列{an}中,a1=1,对所有的n≥2,都有a1·a2·a3·…·an=n2,则a3+a5等于( )
A. | B. | C. | D. |
C
因为a1=1,
当n≥2时,a1·a2·a3·…·an=n2 ①,
所以a1·a2·a3·…·an+1=(n+1)2 ②,
则 得an+1=
得an+1= ,
,
所以a3= =
= ,a5=
,a5= =
= ,
,
所以a3+a5= +
+ =
= =
= .故选C.
.故选C.
当n≥2时,a1·a2·a3·…·an=n2 ①,
所以a1·a2·a3·…·an+1=(n+1)2 ②,
则
 得an+1=
得an+1= ,
,所以a3=
 =
= ,a5=
,a5= =
= ,
,所以a3+a5=
 +
+ =
= =
= .故选C.
.故选C.
练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 (
( )是曲线
)是曲线 上的点,
上的点, ,
, 是数列
是数列 的前
的前 项和,且满足
项和,且满足 ,
, ,
, .
. (
( )是常数数列;
)是常数数列; 的取值集合
的取值集合 ,使
,使 时,数列
时,数列 (
( 的前
的前 项和为
项和为 ,向量
,向量 ,(
,(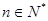 )满足
)满足 .
. 的通项公式为
的通项公式为 (
( ),若
),若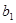 ,
, ,
, (
( )成等差数列,求
)成等差数列,求 和
和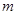 的值;
的值; 满足
满足 ,公比
,公比 满足
满足 ,且对任意正整数
,且对任意正整数 ,
, 仍是该数列中的某一项,求公比
仍是该数列中的某一项,求公比 ,…,则第n个式子是( )
,…,则第n个式子是( )



 为等差数列
为等差数列 的前
的前 项和,
项和, ,则
,则 =
=

