题目内容
如图所示,某建筑工地准备建造一间两面靠墙的三角形露天仓库堆放材料,已知已有两面墙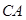 、
、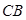 的夹角为
的夹角为 (即
(即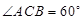 ),现有可供建造第三面围墙的材料
),现有可供建造第三面围墙的材料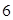 米(两面墙的长均大于
米(两面墙的长均大于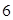 米),为了使得仓库的面积尽可能大,记
米),为了使得仓库的面积尽可能大,记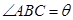 ,问当
,问当 为多少时,所建造的三角形露天仓库的面积最大,并求出最大值?
为多少时,所建造的三角形露天仓库的面积最大,并求出最大值? 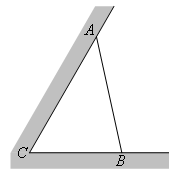
当 时,所建造的三角形露天仓库的面积最大且值为
时,所建造的三角形露天仓库的面积最大且值为 .
.
解析试题分析:先利用正弦定理将边 、
、 表示成
表示成 的代数式,然后利用三角形的面积公式将
的代数式,然后利用三角形的面积公式将 的表示成
的表示成 的三角函数,并借助和差角公式二倍角公式以及辅助角公式对三角函数解析式进行化简,并注意角
的三角函数,并借助和差角公式二倍角公式以及辅助角公式对三角函数解析式进行化简,并注意角 的取值范围,于是将问题转化为三角函数在定区间上的最值问题,利用整体法求解即可.
的取值范围,于是将问题转化为三角函数在定区间上的最值问题,利用整体法求解即可.
在 中,由正弦定理:
中,由正弦定理: ,
,
化简得: ,
, ,
,
所以


 ,
,
即 ,
,
所以当 ,即
,即 时,
时, .
.
答:当 时,所建造的三角形露天仓库的面积最大且值为
时,所建造的三角形露天仓库的面积最大且值为 .
.
考点:1.正弦定理;2.三角形的面积;3.三角函数的最值

练习册系列答案
相关题目
 <φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).
<φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).
 ,求f(2θ)的值.
,求f(2θ)的值. +
+ +
+ (
( 为常数)
为常数) 的最小正周期;
的最小正周期; 上的最大值与最小值之和为
上的最大值与最小值之和为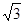 ,求实数
,求实数 的值.
的值. ,
,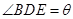 ,
,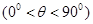 .
.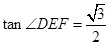 时,求
时,求 的大小;
的大小;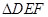 的面积S的最小值及使得S取最小值时
的面积S的最小值及使得S取最小值时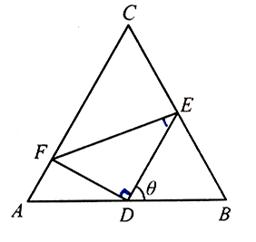
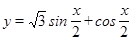 的图像,并说明这个图像是由
的图像,并说明这个图像是由 的图像经过怎样的变换得到的.
的图像经过怎样的变换得到的.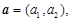
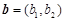 ,定义一种向量积
,定义一种向量积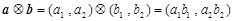 .
.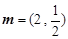 ,
,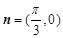 ,点
,点 为
为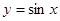 的图象上的动点,点
的图象上的动点,点
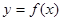 的图象上的动点,且满足
的图象上的动点,且满足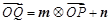 (其中
(其中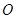 为坐标原点).
为坐标原点).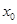 表示
表示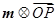 ;
; 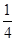 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数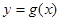 的图象.设函数
的图象.设函数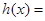
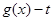
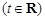 ,试讨论函数
,试讨论函数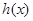 在区间
在区间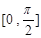 内的零点个数.
内的零点个数.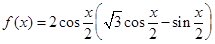 .
.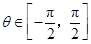 ,且
,且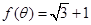 ,求
,求 的值;
的值;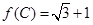 ,且△ABC的面积为
,且△ABC的面积为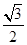 ,求sinA+sinB的值.
,求sinA+sinB的值.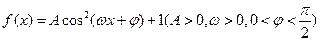 的最大值为3,
的最大值为3, 的图像的相邻两对称轴间的距离为2,在
的图像的相邻两对称轴间的距离为2,在 轴上的截距为2.
轴上的截距为2. (其中ω>0,x∈R)的最小正周期为10π.
(其中ω>0,x∈R)的最小正周期为10π.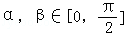 ,
, ,
,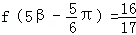 ,求cos(α+β)的值.
,求cos(α+β)的值.