题目内容
平面直角坐标系中,直线![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的两动点,且
上的两动点,且![]() ,求使得四边形
,求使得四边形![]() 周长最小时
周长最小时![]() 两点的坐标及此时的最小周长
两点的坐标及此时的最小周长
![]() ,
,![]() 时,四边形周长最小,且最小周长为
时,四边形周长最小,且最小周长为![]()
解析:
如图:
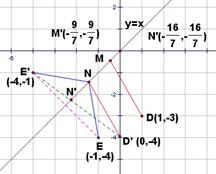 |
周长![]()
故当![]() 最小时,周长最小
最小时,周长最小
将![]() 平移至
平移至![]() ,则
,则![]() ,
,![]()
作![]() 关于
关于![]() 的对称点
的对称点![]() ,连接
,连接![]()
则![]()
![]()
当且仅当![]() 三点共线时,
三点共线时,![]() 取得最小值
取得最小值![]()
此时,![]() 方程为
方程为![]() ,与
,与![]() 交点坐标为
交点坐标为![]() ,
,![]()
故当![]() ,
,![]() 时,四边形周长最小,且最小周长为
时,四边形周长最小,且最小周长为![]()

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
 如图,平面直角坐标系中,A(
如图,平面直角坐标系中,A(
 ,2),B(-
,2),B(- ,-
,-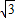 ),将其所在纸面沿x轴折成直二面角,则折起后的A,B两点的距离是 .
),将其所在纸面沿x轴折成直二面角,则折起后的A,B两点的距离是 .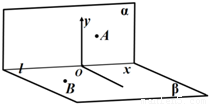
 ,2),B(-
,2),B(- ,-
,- ),将其所在纸面沿x轴折成直二面角,则折起后的A,B两点的距离是 .
),将其所在纸面沿x轴折成直二面角,则折起后的A,B两点的距离是 .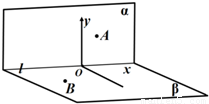
 ,2),B(-
,2),B(- ,-
,-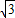 ),将其所在纸面沿x轴折成直二面角,则折起后的A,B两点的距离是 .
),将其所在纸面沿x轴折成直二面角,则折起后的A,B两点的距离是 .