题目内容

（2011•潍坊二模）抛物线的顶点在坐标原点，焦点与双曲线
y2
5
-
x2
4
=1的一个焦点重合，则该抛物线的标准方程可能是（　　）
分析：由题意可知双曲线
y2
5
-
x2
4
=1的焦点为（0，3），（0，-3），从而所求抛物线的焦点可知，即可求解
解答：解：∵双曲线
y2
5
-
x2
4
=1的焦点为（0，3），（0，-3）
当所求的抛物线的焦点为（0，3）时，抛物线方程为x2=12y
当所求的抛物线的焦点为（0，-3）时，抛物线方程为x2=-12y
结合选项可知，选项D正确
故选D
点评：本题主要考查了双曲线的性质的应用及由焦点坐标求解抛物线的方程，属于基础试题
练习册系列答案
相关题目
（2011•潍坊二模）设p：
xx-2
＜0，q：0＜x＜m，若p是q成立的充分不必要条件，则m的取值范围是
（2，+∞）
（2，+∞）
．
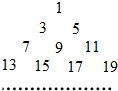（2011•潍坊二模）已知数列an=2n-1（n∈N*），把数列{an}的各项排成如图所示的三角形数阵，记（m，n）表示该数阵中第m行中从左到右的第n个数，则S（10，6）对应于数阵中的数是
101
101
．
（2011•潍坊二模）已知
m
=(cos?x，sin?x)，
n
=(cos?x，2
3
cos?x-sin?x)，?＞0，函数f(x)=
m
•
n
+|
m
|，x1，x2是集合M={x|f（x）=1}中任意两个元素，且|x1-x2|的最小值为
π
2
．
（1）求?的值．
（2）在△ABC中，a，b，c分别是A，B，C的对边．f(A)=2，c=2，S△ABC=
3
2
，求a的值．
（2011•潍坊二模）运行如图的程序框图，当输入m=-4时的输出结果为n，若变量x，y满足
x+y≤3
x-y≥-1
y≥n
，则目标函数z=2x+y的最大值为
5
5
．
（2011•潍坊二模）已知偶函数f（x）对?x∈R满足f（2+x）=f（2-x）且当-2≤x≤0时，f（x）=log2（1-x），则f（2011）的值为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网