题目内容
在极坐标方程中,曲线C的方程是ρ=4sinθ,过点(4, )作曲线C的切线,则切线长为( )
)作曲线C的切线,则切线长为( )
| A.4 | B. | C.2 | D.2 |
C
解析试题分析:根据题意,由于曲线C的方程是ρ=4sinθ,则可知ρ =4ρsinθ,故可知
=4ρsinθ,故可知 在可知曲线C为圆的方程,圆心(0,2),半径为2,则可知过点(4,
在可知曲线C为圆的方程,圆心(0,2),半径为2,则可知过点(4, )即为点(2
)即为点(2 ,2)作曲线C的切线,则可知圆心到点(2
,2)作曲线C的切线,则可知圆心到点(2 ,2)的距离为d=2
,2)的距离为d=2 ,圆的半径为2,那么利用勾股定理可知,则切线长为2
,圆的半径为2,那么利用勾股定理可知,则切线长为2 ,选C。
,选C。
考点:极坐标方程
点评:主要是考查了极坐标方程的运用,属于基础题。

练习册系列答案
相关题目
直线 和圆
和圆 交于
交于 两点,则
两点,则 的中点坐标为
的中点坐标为
A. | B. | C. | D. |
点 的直角坐标是
的直角坐标是 ,则点
,则点 的极坐标为( )
的极坐标为( )
A. | B. | C. | D. |
在极坐标系中,点A(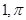 )到直线
)到直线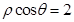 的距离是( ).
的距离是( ).
| A.1 | B.2 | C.3 | D.4 |
曲线的极坐标方程 化成直角坐标方程为( )
化成直角坐标方程为( )
A. | B. |
C. | D. |
在极坐标系中,与点 关于极点对称的点的坐标是 ( )
关于极点对称的点的坐标是 ( )
A. | B. | C. | D. |
极坐标系中,以(9, )为圆心,9为半径的圆的极坐标方程为( )
)为圆心,9为半径的圆的极坐标方程为( )
A. | B. |
C. | D. |
 (t为参数),若以直角坐标系的原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为_______________.
(t为参数),若以直角坐标系的原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为_______________.