题目内容
8、已知函数f（x）=|log2|x-1||，且关于x的方程[f（x）]2+af（x）+2b=0有6个不同的实数解，若最小的实数解为-1，则a+b的值为（ ）
分析：先作出函数f（x）=|log2|x-1||的图象，令t=f（x），方程[f（x）]2+af（x）+2b=0转化为：t2+at+2b=0，再方程[f（x）]2+af（x）+2b=0有6个不同的实数解，可知方程t2+at+2b=0有一零根和一正根，又因为最小的实数解为-1，所以f（-1）=1从而得到方程：t2+at+2b=0的两根是0和1，最后由韦达定理求得得：a，b进而求得a+b．
解答：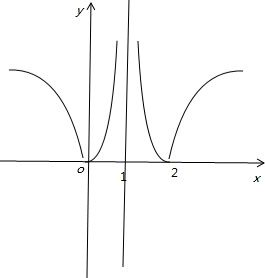
解：作出函数f（x）=|log2|x-1||的图象
∵方程[f（x）]2+af（x）+2b=0有6个不同的实数解
∴如图所示：令t=f（x），
方程[f（x）]2+af（x）+2b=0转化为：t2+at+2b=0
则方程有一零根和一正根，
又∵最小的实数解为-1
∴f（-1）=1
∴方程：t2+at+2b=0的两根是0和1
由韦达定理得：a=-1，b=0
∴a+b=-1
故选B
解：作出函数f（x）=|log2|x-1||的图象∵方程[f（x）]2+af（x）+2b=0有6个不同的实数解
∴如图所示：令t=f（x），
方程[f（x）]2+af（x）+2b=0转化为：t2+at+2b=0
则方程有一零根和一正根，
又∵最小的实数解为-1
∴f（-1）=1
∴方程：t2+at+2b=0的两根是0和1
由韦达定理得：a=-1，b=0
∴a+b=-1
故选B
点评：本题主要考查函数与方程的综合运用，还考查了方程的根与函数零点的关系．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|