Question

已知函数f(x)=.

(1)在函数y=f(x)的图象上是否存在一点(m,n),使得y=f(x)的图象关于(m,n)对称?

(2)设y=f^-1(x)为y=f(x)的反函数,令g(x)=f^-1(),是否存在这样的实数b,使得任意的a∈［, ］时,对任意的x∈(0,+∞),不等式g(x)＞x-ax²+b恒成立?若存在,求出b的取值范围;若不存在,说明理由.

Answer 1

解:(1)若存在一点(m,n),使得y=f(x)的图象关于点(m,n)对称,

则f(x+m)+f(m-x)=2n.1分

∴+===2n,

当2e^2m=e^2m+1时,2n=1?m=0,n=,且(0, )在y=f(x)的图象上,

∴在y=f(x)的图象上存在一点(0, ),使得y=f(x)的图象关于(0, )对称.

(2)f(x)===1,∴e^x+1=.∴x=ln.

∴f^-1(x)=ln(0＜x＜1).

∴g(x)=f^-1()=ln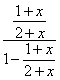=ln(x+1)(x＞-1).

构造函数F(x)=ln(1+x)-x+ax²,

则F′(x)=+2ax-1==,

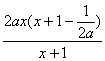∵x＞0,a∈［,］,∴x+1＞0,2ax＞0.

若F′(x)＜0,则x∈(0, a-1),

∴F(x)在(0, a-1)上是减函数;

若F′(x)＞0,则x∈(-1,+∞),

∴F(x)在(-1,+∞)上是增函数.

∵函数F(x)在(0,+∞)上是连续函数,

∴当x=-1时,F(x)取最小值,

即F(x)_min=F(-1)=ln-+1+a(-1)²

=ln-+1++a-1=ln-+a.

记h(a)=ln-a+a,

又h′(a)=2a×(-)++1=+1=(-2)²,

∵∈［3,4］,∴h′(a)＞0,即h(a)在［,］上为增函数.

∴h(a)_min=h()=ln2.

∴若使F(x)＞b恒成立,只需b＜ln2.

∴存在这样的实数b＜ln2,使得对a∈［,］,对任意的x∈(0,+∞)时,不等式ln(1+x)＞x-ax²+b恒成立.