题目内容
已知二次函数f(x)=ax2+bx+c(a,b,c为实数a不为零),且同时满足下列条件:
(1)f(-1)=0;
(2)对于任意的实数x,都有f(x)-x≥0;
(3)当x∈(0,2)时有 .
.
①求f(1);
②求a,b,c的值;
③当x∈[-1,1]时,函数g(x)=f(x)-mx(m∈R)是单调函数,求m的取值范围.
解:(1)当x=1时,由 f(1)-1≥0,且 =1,∴f(1)=1.
=1,∴f(1)=1.
(2)设二次函数为f(x)=ax2+bx+c,由f(-1)=0可得a-b+c=0,
而f(1)=1,∴ .
.
又f(x)-x≥0,∴ax2+bx+c-x≥0,化简得 ax2+(b-1)x+c≥0,
∴a>0且(b-1)2-4ac≤0,把 ,代入化简可得
,代入化简可得  ,
,
∴ .
.
(3)由上可得 f(x)=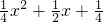 ,∴
,∴ -mx=
-mx= ,
,
因为函数g(x)在[-1,1]上单调可知,- ≤-1,或-
≤-1,或- ≥1,
≥1,
解得m≤0,或m≥1.故m的取值范围是{m|m≤0,或m≥1}.
分析:(1)当x=1时,根据f(1)-1≥0,且 =1,可得f(1)=1.
=1,可得f(1)=1.
(2)由f(-1)=0 和f(1)=1,可得 b= =a+c,再由f(x)-x≥0,可得 a=c=
=a+c,再由f(x)-x≥0,可得 a=c= .
.
(3)由上可得 f(x)=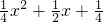 ,求出g(x)的解析式,由函数g(x)在[-1,1]上单调可知,
,求出g(x)的解析式,由函数g(x)在[-1,1]上单调可知,
有- ≤-1,或-
≤-1,或- ≥1,解不等式求得m的取值范围.
≥1,解不等式求得m的取值范围.
点评:本题考查求函数的值的方法,二次函数的单调性的应用,体现了分类讨论的数学思想,求出a,b,c的值,是解题的
关键.
 =1,∴f(1)=1.
=1,∴f(1)=1.(2)设二次函数为f(x)=ax2+bx+c,由f(-1)=0可得a-b+c=0,
而f(1)=1,∴
 .
.又f(x)-x≥0,∴ax2+bx+c-x≥0,化简得 ax2+(b-1)x+c≥0,
∴a>0且(b-1)2-4ac≤0,把
 ,代入化简可得
,代入化简可得  ,
,∴
 .
.(3)由上可得 f(x)=
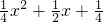 ,∴
,∴ -mx=
-mx= ,
,因为函数g(x)在[-1,1]上单调可知,-
 ≤-1,或-
≤-1,或- ≥1,
≥1,解得m≤0,或m≥1.故m的取值范围是{m|m≤0,或m≥1}.
分析:(1)当x=1时,根据f(1)-1≥0,且
 =1,可得f(1)=1.
=1,可得f(1)=1.(2)由f(-1)=0 和f(1)=1,可得 b=
 =a+c,再由f(x)-x≥0,可得 a=c=
=a+c,再由f(x)-x≥0,可得 a=c= .
.(3)由上可得 f(x)=
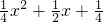 ,求出g(x)的解析式,由函数g(x)在[-1,1]上单调可知,
,求出g(x)的解析式,由函数g(x)在[-1,1]上单调可知,有-
 ≤-1,或-
≤-1,或- ≥1,解不等式求得m的取值范围.
≥1,解不等式求得m的取值范围.点评:本题考查求函数的值的方法,二次函数的单调性的应用,体现了分类讨论的数学思想,求出a,b,c的值,是解题的
关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目