题目内容
设f(x)=ax2+bx+c(a>b>c),f(1)=0,g(x)=ax+b,
(1)求证:函数y=f(x)与y=g(x)的图象有两个交点.
(2)设f(x)与g(x)的图象的交点A,B在x轴上的射影为A1,B1,求|A1B1|的取值范围.
(3)求证:当x≤- 时,恒有f(x)>g(x).
时,恒有f(x)>g(x).
答案:
解析:
解析:
|
解:(1) (2)设方程(*)的两根为x1,x2,则 而|A1B1|=|x1-x2|= (3)令F(x)=f(x)-g(x)=ax2-(2a+c)x+a+2c,因为x≤- |

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
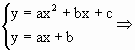 ax2+bx+c=ax+b,即ax2+(b-a)x+c-b=0,(*)其判别式Δ=(b-a)2-4a(c-b).由f(1)=a+b+c=0且a>b>c,知a>0,c-b<0,从而Δ>0,命题得证.
ax2+bx+c=ax+b,即ax2+(b-a)x+c-b=0,(*)其判别式Δ=(b-a)2-4a(c-b).由f(1)=a+b+c=0且a>b>c,知a>0,c-b<0,从而Δ>0,命题得证.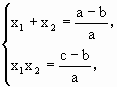
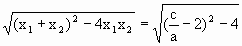 .因为a>b>c,a+b+c=0
.因为a>b>c,a+b+c=0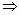 a>0,1>
a>0,1>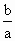 >
>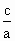 ,即1>
,即1>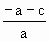 >
>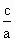 ,所以-2<
,所以-2<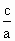 <-
<-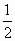 .从而
.从而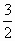 <|A1B1|<2
<|A1B1|<2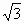 .
.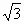 ,所以x2≥3,且-x≥
,所以x2≥3,且-x≥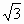 >1.又因为2a+c>0,所以-x(2a+c)≥2a+c.所以F(x)>3a+(2a+c)+(a+2c)=3(2a+c)>0.即F(x)>0,所以当x≤-
>1.又因为2a+c>0,所以-x(2a+c)≥2a+c.所以F(x)>3a+(2a+c)+(a+2c)=3(2a+c)>0.即F(x)>0,所以当x≤-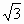 时,恒有f(x)>g(x).
时,恒有f(x)>g(x).