题目内容
有4位学生和3位老师站在一排拍照,任何两位老师不站在一起的不同排法共有
- A.(4!)2种
- B.4!•3!种
- C.A43•4!种
- D.A53•4!种
D
分析:本题要求任何两位老师不站在一起,可以采用插空法,先排4位学生,再使三位教师在学生形成的五个空上排列,最后根据分步计数原理得到结果.
解答:∵要求任何两位老师不站在一起,
∴可以采用插空法,
先排4位学生,有A44种结果,
再使三位教师在学生形成的五个空上排列,有A53种结果,
根据分步计数原理知共有A44A53种结果,
故选D.
点评:站队问题是排列组合中的典型问题,解题时要先排限制条件多的元素,把限制条件比较多的元素排列后,再排没有限制条件的元素,最后要用分步计数原理得到结果.
分析:本题要求任何两位老师不站在一起,可以采用插空法,先排4位学生,再使三位教师在学生形成的五个空上排列,最后根据分步计数原理得到结果.
解答:∵要求任何两位老师不站在一起,
∴可以采用插空法,
先排4位学生,有A44种结果,
再使三位教师在学生形成的五个空上排列,有A53种结果,
根据分步计数原理知共有A44A53种结果,
故选D.
点评:站队问题是排列组合中的典型问题,解题时要先排限制条件多的元素,把限制条件比较多的元素排列后,再排没有限制条件的元素,最后要用分步计数原理得到结果.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
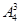 ·4!种 (D)
·4!种 (D)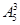 ·4!种
·4!种