Question

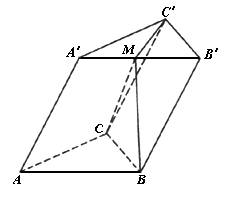
如图，棱柱ABC-A₁B₁C₁中，A₁A，A₁B，A₁C都与平面ABC所成的角相等，∠CAB=90°，AC=AB=A₁B=a，D为BC上的点，且A₁C∥平面ADB₁．求：
（Ⅰ）A₁C与平面ADB₁的距离；
（Ⅱ）二面角A₁-AB-C的大小；
（Ⅲ）AB₁与平面ABC所成的角的大小．

Answer 1

分析：解法一：
（1）求直线到平面的距离的距离通常可以转化成点到平面的距离．根据三棱柱的结构特征可证明：A₁E⊥平面ADE，所以A₁E为点A₁到平面ADE的距离，即A₁C与平面ADB₁的距离；
（2）二面角的度量关键在于作出它的平面角，常用的方法就是三垂线定理．因为棱柱ABC-A₁B₁C₁中，A₁A，A₁B，A₁C都与平面ABC所成的角相等，∠CAB=90°，AC=AB=A₁B=a，D为BC上的点，则A₁D⊥平面ABC，过D作DG⊥AB，连A₁G，则A₁G⊥AB，∠A₁DG为二面角A₁-AB-C的平面角．
（3）直线与平面所成的角，首先要找出垂直于平面的直线，取BD中点F，连EF∥A₁D，又由（1）可知：A₁D⊥平面ABC，所以EF⊥平面ABC，连AF，则∠EAF为A₁B与平面ABC所成的角．
解法二：（向量法）
分别以AB、AC为x、y轴，平面ABC的垂线为z轴，建立空间直角坐标系，则A（0，0，0）B（a，0，0），C（0，a，0），连A₁B，由条件知，△A₁AB和△A₁AC均为等边△且边长为a，所以∠A₁AB=∠A₁AC=60°，设A（x，y，z），根据余弦定理可得：A(

1

2

a，

1

2

a，

2

2

a)，设A1B与AB1相交与E，则

AE

=

1

2

(

AA1

+

AB

)=(

3

4

a，

1

4

a，

2

4

a)．这种解法的好处就是（1）解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理，因为这些可以用向量方法来解决．（2）即使立体感稍差一些的学生也可以顺利解出，因为只需画个草图以建立坐标系和观察有关点的位置即可．
（1）求A₁C与平面ADB₁的距离，可设面ADB₁的法向量

v

=(x，y，z)，取

v

=(-a，a，

2

a)，设A₁C面ADB₁的距离为d，则d=

| AA1 • v |

| v |

=

a2

2a

=

1

2

a．
（2）平面ABC的一个法向量为

m

=(0，0，a)，设平面A₁AB的法向量为

n

=(x，y，z)，则这两个法向量的夹角的大小即为二面角A₁-AB-C的大小．
（3）由（2）可知：AB₁与平面ABC所成的角的大小即为平面ABC的一个法向量与

AE

的夹角的大小．

解答：解：（I）设A₁B与AB₁的交点为E，连DE
∵A₁C∥平面ADE，
∴A₁C∥DE且A₁C到平面ADE的距离等于点A₁到平面ADE的距离
又∵△CA₁B≌△CAB，
∴∠CA₁B=90°，
即CA₁⊥A₁B
∴A₁E⊥ED，又A₁E⊥AE
∴A₁E⊥平面ADE
∴A₁E为点A₁到平面ADE的距离，又A1E=

1

2

a
∴A₁C到平面ADB的距离等于

1

2

a
（Ⅱ）∵A₁ABB₁为平行四边形，
∴A₁E=EB，又A₁C∥DE
∴D为BC中点
∵A₁A，A₁B，A₁C与平面ABC所成角相等
∴A₁A=A₁B=A₁C，
∴点A₁在平面ABC的射影为Rt△ABC的外心，
又RtABC外心为斜边中点D，连A₁D，则A₁D⊥平面ABC
过D作DG⊥AB，连A₁G，
则A₁G⊥AB，∠A₁DG为二面角A₁-AB-C的平面角
∵DG∥CA，
∴DG=

1

2

AC=

1

2

a，
即二面角A₁-AB-C的大小为arccos

3

3

（Ⅲ）取BD中点F，连EF∥A₁D，
∵A₁D⊥平面ABC，
∴EF⊥平面ABC，连AF，
则∠EAF为A₁B与平面ABC所成的角
在Rt△ADA₁中，A1D=

A1A2-AD2

=

2

2

a，
∴EF=

1

2

A1D=

2

4

a，又AE=

3

2

a，sin∠EAF=

EF

AE

=

6

6

即AB₁与平面ABC所成的角为arcsin

6

6

解法二：（向量法）建立如图坐标系，则A（0，0，0）B（a，0，0），C（0，a，0）
连A₁B，由条件知，△A₁AB和△A₁AC均为等边△且边长为a，
∴∠A₁AB=∠A₁AC=60°，设A（x，y，z），
则

AA1

=(x，y，z)
由

AA1

•

AB

=|

AA1

|•|

AB

|cos∠A1AB?ax=

1

2

a2?x=

1

2

a
同理得y=

1

2

a，由|

AA1

|=a得x2+y2+z 2=a2?z=

2

2

a
∴A(

1

2

a，

1

2

a，

2

2

a)，设A1B与AB1相交与E，则

AE

=

1

2

(

AA1

+

AB

)=(

3

4

a，

1

4

a，

2

4

a)
（I）A₁C∥面ADB₁，
∵A₁C∥ED，又E为A₁B中点，
∴D为BC中点，
∴D(

a

2

，

a

2

，0)，

AD

=(

a

2

，

a

2

，0)，
设面ADB₁的法向量

v

=(x，y，z)
则

v • AD =0 v • AE =0

?

a 2 x+ a 2 y=0 3a 4 x+ 1 4 ay+ 2 4 az=0

取

v

=(-a，a，

2

a)
设A₁C面ADB₁的距离为d，则d=

| AA1 • v |

| v |

=

a2

2a

=

1

2

a
（Ⅱ）平面ABC的一个法向量为

m

=(0，0，a)，
设平面A₁AB的法向量为

n

=(x，y，z)
则

n • AB =0 n • AA1 =0

?

ax=0 1 2 ax+ 1 2 ay+ 2 2 ax=0

，
取

n

=(0，-

2

a，a)
设

m

，

n

的夹角为θ1，则cosθ1=

m • n

| m |•| n |

=

3

3

即二面角A₁-AB-C的大小为arccos

3

3

（Ⅲ）设AB₁与平面ABC所成角为θ₂，
则sinθ2=|cosθ|=

| m • AE |

| m |•| AE |

=

2 4 a2

3 2 a2

=

6

6

∴θ2=arcsin

6

6

，
即AB₁与平面ABC所成角为arcsin

6

6

点评：本小题主要考查棱柱的结构特征，二面角及其度量，直线与平面所成的角，空间中点、线、面的距离计算和线面关系等基本知识，同时考查空间想象能力和推理、运算能力．