题目内容
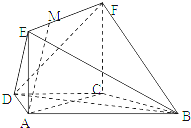 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.(1)求证:BC⊥平面ACFE;
(2)当EM为何值时,AM∥平面BDF?写出结论,并加以证明.
(3)当EM为何值时,AM⊥BE?写出结论,并加以证明.
分析:(1)根据线面垂直的判定定理,即可证明:BC⊥平面ACFE;
(2)根据线面平行的判定定理,确定EM的长度,然后根据AM∥平面BDF的判定定理即可得到结论.
(3)要证明AM⊥BE,则只需证明AM⊥平面BCE即可得到结论.
(2)根据线面平行的判定定理,确定EM的长度,然后根据AM∥平面BDF的判定定理即可得到结论.
(3)要证明AM⊥BE,则只需证明AM⊥平面BCE即可得到结论.
解答:(1)证明:在梯形ABCD中,∵AB∥CD,AD=DC=CB=a,∠ABC=60°,
∴四边形ABCD是等腰梯形,
且∠DCA=∠DAC=30°,∠DCB=120°,
∴∠ACB=∠DCB-∠DCA=90°,
∴AC⊥BC
又∵平面ACFE⊥平面ABCD,交线为AC,
∴BC⊥平面ACFE
(2)当EM=
a时,AM∥平面BDF,
在梯形ABCD中,设AC∩BD=N,连接FN,则CN:NA=1:2,
∵EM=
a、而EF=AC=
a,
∴EM:MF=1:2,
∴MF
AN,∴四边形ANFM是平行四边形,∴AM∥NF
又∵NF?平面BDF,AM?平面BDF∴AM∥平面BDF,
(3)连结CE,由1)知BC⊥平面ACFE,
∴BC⊥AM
当AM⊥CE时△AEM∽△CAE有
=
即
=
得EM=
a,
∴当EM=
a时AM⊥CE,即AM⊥平面BCE,也即AM⊥BE.
∴四边形ABCD是等腰梯形,

且∠DCA=∠DAC=30°,∠DCB=120°,
∴∠ACB=∠DCB-∠DCA=90°,
∴AC⊥BC
又∵平面ACFE⊥平面ABCD,交线为AC,
∴BC⊥平面ACFE
(2)当EM=
| ||
| 3 |
在梯形ABCD中,设AC∩BD=N,连接FN,则CN:NA=1:2,
∵EM=
| ||
| 3 |
| 3 |
∴EM:MF=1:2,
∴MF
| ||
. |
又∵NF?平面BDF,AM?平面BDF∴AM∥平面BDF,
(3)连结CE,由1)知BC⊥平面ACFE,
∴BC⊥AM
当AM⊥CE时△AEM∽△CAE有
| AC |
| AE |
| AE |
| EM |
| ||
| a |
| a |
| EM |
| ||
| 3 |
∴当EM=
| ||
| 3 |
点评:本题主要考查空间直线和平面平行或垂直的位置关系的判断,要求熟练掌握常用的判定定理和性质定理.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
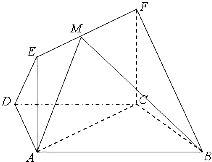 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.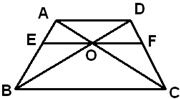 如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF=
如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF= 如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出
如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出 如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.