题目内容
如图,点A在锐二面角α-MN-β的棱MN上,在面α内引射线AP,使AP与MN所成的角∠PAM为45°,与面β所成的二面角大小为30°,求二面角α-MN-β的大小.

答案:略
解析:
提示:
解析:
|
解:在射线 AP上取一点B,作BH⊥β于H,连结AH,则∠BAH为射线AP与平面β所成的角,∴∠BAH=30°再作BQ⊥AM,交MN于Q,连结HQ,则HQ为BQ在平面β内的射影.由三垂线定理的逆定理,知HQ⊥MN,∴∠ BQH为二面角α-NM-β的平面角.设 BQ=a,在Rt△BAQ中,∠BAQ=90°,∠BAM=45°, , ,
∴在 Rt△ABH中,∠BAH=30°,∴  . .
∴在 Rt△BHQ中,∠BHQ=90°,BQ=a , , ,
∵∠ BQH是锐角,∴∠BQH=45°,即二面角α-NM-β等于45° |
提示:
|
首先根据条件作出二面角的平面角,然后将平面角放入一个可解的三角形中 (最好是直角三角形),通过解三角形使问题得到解决.本题综合性较强,在一个图形中出现了两条直线所成的角,斜线与平面所成的角,二面角等空间角,这些空间角都要转化为平面角,而且还要彼此联系相互依存,要根据各自的定义添加适当的辅助线. |

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目

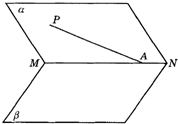 如图,点A在锐二面角α-MN-β的棱MN上,在面α内引射线AP,使AP与MN所成的∠PAM为45°,与面β所成的角为30°,求二面角α-MN-β的大小
如图,点A在锐二面角α-MN-β的棱MN上,在面α内引射线AP,使AP与MN所成的∠PAM为45°,与面β所成的角为30°,求二面角α-MN-β的大小

