题目内容
某交警部门对城区上下班交通情况作抽样调查，上下班时间各抽取12辆机动车的行驶速度（单位：km/h）作为样本进行研究，做出样本的茎叶图，则上班、下班时间行驶速度的中位数分别是（ ）
| A．2827.5 | B．2828.5 |
| C．2927.5 | D．2928.5 |
C
解析试题分析：据已知中的茎叶图，我们易得到左右两边两组数据的值，然后根据中位数的定义，即可得到答案．解：由已知中茎叶图，我们易得左右两边的数据分别为：左：18，20，21，26，27，28，30，32，33，35，36，40；右：16，17，19，22，25，27，28，30，30，32，36，37；左右两边的中位数分别为：
，故可知选C.
考点：中位数、茎叶图
点评：本题考查的知识点是中位数、茎叶图，其中根据茎叶图分析出两组数据是解答本题的关键．
阅读快车系列答案某校共有学生2000名，各年级男、女生人数如下表．已知在全校 学生中随机抽取1名，抽到二年级女生的概率是0．19．现用分层抽样的方法在全校抽取64名学生，则应在三年级抽取的学生人数为 ．
| | 一年级 | 二年级 | 三年级 |
| 女生 | 373 |  |  |
| 男生 | 377 | 370 |  |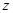
在样本的频率分布直方图中,共有11个小长方形,若中间一个小长立形的面积等于其他10个小长方形的面积的和的
,且样本容量为160,则中间一组有频数为 ( )
| A．32 | B．0.2 | C．40 | D．0.25 |
在回归分析中，代表了数据点和它在回归直线上相应位置的差异的是（ ）
| A．总偏差平方和 | B．残差平方和 | C．回归平方和 | D．相关指数R2 |
设某大学的女生体重y(单位：kg)与身高x(单位：cm)具有线性相关关系，根据一组样本数据(xi，yi)(i＝1,2，…，n)，用最小二乘法建立的回归方程为
＝0.85x－85.71，则下列结论中不正确的是( )．
| A．y与x具有正的线性相关关系 |
B．回归直线过样本点的中心( ， ) |
| C．若该大学某女生身高增加1 cm，则其体重约增加0.85 kg |
| D．若该大学某女生身高为170 cm，则可断定其体重必为58.79 kg |
通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的
列联表：
| | 男 | 女 | 总计 |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
算得，
附表：
 | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
有99%以上的把握认为“爱好该项运动与性别有关”
有99%以上的把握认为“爱好该项运动与性别无关”
在犯错误的概率不超过0.1%的前提下，认为 “爱好该项运动与性别有关”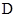
在犯错误的概率不超过0.1%的前提下，认为 “爱好该项运动与性别无关” 两个变量x，y与其线性相关系数r有下列说法
（1）若r>0，则x增大时，y也相应增大；
（2）若|r|越趋近于1，则x， y线性相关程度越强；
（3）若r＝1或r＝－1，则x与y的关系完全对应(有函数关系)，在散点图上各个散点均在一条直线上，其中正确的有（ ）
| A．①② | B．②③ | C．①③ | D．①②③ |
一个单位有职工800人，期中具有高级职称的160人，具有中级职称的320人，具有初级职称的200人，其余人员120人.为了解职工收入情况，决定采用分层抽样的方法，从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是( )
| A．12,24,15,9 | B．9,12,12,7 |
| C．8,16,10,6 | D．8,15,12,5 |
设其平均数为a,中位数为
,众数为
，则有 ( )
