题目内容
设a，b，c为一个三角形的三边，
，且s2=2ab，试证：s＜2a．
解：∵a，b，c为一个三角形的三边，∴a+c＞b． 又 ，
∴s＞b，∴s2＞sb．
又s2=2ab，∴2ab＞sb，
∴s＜2a．
分析：由a，b，c为一个三角形的三边，可得a+c＞b，s＞b，故s2＞sb，即2ab＞sb，从而证得s＜2a．
点评：本题考查三角形的任意两边之和大于第三边，不等式的性质的应用，证得s＞b，是解题的关键．
，∴s＞b，∴s2＞sb．
又s2=2ab，∴2ab＞sb，
∴s＜2a．
分析：由a，b，c为一个三角形的三边，可得a+c＞b，s＞b，故s2＞sb，即2ab＞sb，从而证得s＜2a．
点评：本题考查三角形的任意两边之和大于第三边，不等式的性质的应用，证得s＞b，是解题的关键．
练习册系列答案
相关题目
、b+
、c+
这三个数 
，则称函数f（x）为上凸函数． 若函数f（x）为上凸函数，则对定义域内任意x1、x2、x3，…，xn都有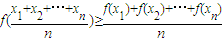
（当x1=x2=x3=…=xn时等号成立），称此不等式为琴生不等式，现有下列命题：
；
．