题目内容
设函数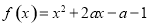
，
，
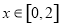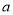为常数.
（1）用
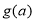表示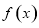
的最小值，求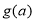的解析式；
（2）在（1）中，是否存在最小的整数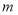
，使得
对于任意
均成立，若存在，求出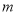
的值；若不存在，请说明理由.
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
字词句篇与同步作文达标系列答案题目内容
设函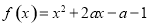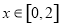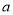数，，为常数.
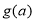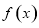（1）用表示的最小值，求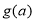的解析式；
（2）在（1）中，是否存在最小的整数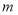，使得对于任意均成立，若存在，求出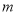的值；若不存在，请说明理由.
字词句篇与同步作文达标系列答案
，
．
；
，
，有
，
，求证：
．
是定义在
上的奇函数，当
时，
，则
（ ）
的定义域是（ ）
B．
D．
在区间
上单调递减，则实数
的取值范围是 .
为R上的减函数，则实数a的取值范围是（ ）
B.
D.
有两个不同的极值点，那么实数
的范围是 ．
中，
,且
.
的通项公式；
成等比数列，求数列
的前
项和
.