题目内容
函数
 ,当
,当 时,恒有
时,恒有 ,有( )
,有( )
A.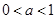 且 且 在 在 上是增函数 上是增函数 |
B.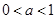 且 且 在 在 上是减函数 上是减函数 |
C. 且 且 在 在 上是增函数 上是增函数 |
D. 且 且 在 在 上是减函数 上是减函数 |
A
解析试题分析:当 时,
时, ,且
,且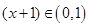
 ,此时又有
,此时又有 ,所以
,所以 当
当 时,
时, ,
, ,此时根据复合函数的单调性知
,此时根据复合函数的单调性知 在
在 上是增函数.
上是增函数.
考点:此题主要考查复合函数的单调性.
点评:复合函数的单调性一直是一个重要的考点,要正确解答此类题目,学生要正确分析出组成复合函数的两个函数分别是什么,它们的单调性是怎样的,然后根据复合函数的单调性同增异减的性质,准确判断出所给函数的单调性以及其中参数的取值范围,另外还要注意定义域的要求.

练习册系列答案
相关题目
下列幂函数中过点 ,
, 的偶函数是 ( )
的偶函数是 ( )
A. | B. | C. | D. |
设
A. | B.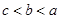 | C. | D. |
函数
 的值域是( )
的值域是( )
A. | B. | C. | D. |
如果函数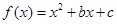 对任意实数
对任意实数 都有
都有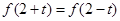 ,那么( )
,那么( )
A. < < < < | B. < < < < |
C. < < < < | D. < < < < |
如果对数函数 在
在 上是减函数,则
上是减函数,则 的取值范围是
的取值范围是
A. | B. | C. | D. |
若函数 ,则
,则 的值为 ( )
的值为 ( )
| A.5 | B.-1 | C.-7 | D.2 |
若函数 是幂函数,则
是幂函数,则 的值为( )
的值为( )
A. | B. | C.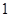 | D. |
 ,二次函数
,二次函数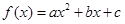 的图像可能是
的图像可能是 


