题目内容
已知数列an=2n,前n项和为Sn,若数列{
}的前n项和为Tn,则T2012的值为( )
| 1 |
| Sn |
A.
| B.
| C.
| D.
|
∵数列an=2n,∴数列{an}是一个等差数列,∴前n项和Sn=
=n2+n.
∴
=
=
-
,
∴Tn=(1-
)+(
-
)+…+(
-
)=1-
=
.
∴T2012=
.
故选D.
| n(2+2n) |
| 2 |
∴
| 1 |
| Sn |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
∴T2012=
| 2012 |
| 2013 |
故选D.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知数列an=-2n+12,Sn为其前n项和,则Sn取最大值时,n值为( )
| A、7或6 | B、5或6 | C、5 | D、6 |
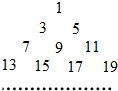 (2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是
(2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是