题目内容
(2010•舟山模拟)一个半径为1的小球在一个棱长为4
的正四面体容器内可向各个方向自由运动,则该小球永远不可能接触到的容器内壁的面积是
| 6 |
72
| 3 |
72
.| 3 |
分析:小球与正四面体的一个面相切时的情况,易知小球在面上最靠近边的切点的轨迹仍为正三角形,正四面体的棱长为4
,故小三角形的边长为2
,做出面积相减,得到结果.
| 6 |
| 6 |
解答:解:考虑小球与正四面体的一个面相切时的情况,
易知小球在面上最靠近边的切点的轨迹仍为正三角形,
正四面体的棱长为4
故小三角形的边长为2
小球与一个面不能接触到的部分的面积为
×4
×4
×
-
×2
×2
×
=18
,
∴几何体中的四个面小球永远不可能接触到的容器内壁的面积是4×18
=72
故答案为:72
易知小球在面上最靠近边的切点的轨迹仍为正三角形,
正四面体的棱长为4
| 6 |
故小三角形的边长为2
| 6 |
小球与一个面不能接触到的部分的面积为
| 1 |
| 2 |
| 6 |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| 6 |
| 6 |
| ||
| 2 |
| 3 |
∴几何体中的四个面小球永远不可能接触到的容器内壁的面积是4×18
| 3 |
| 3 |
故答案为:72
| 3 |
点评:本题考查棱柱的结构特征,本题解题的关键是看出小球的运动轨迹是什么,看出是一个正三角形,这样题目做起来就方向明确.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
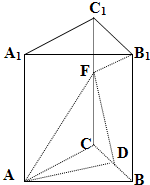 (2010•舟山模拟)在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是CC1上一点,且CF=2a.
(2010•舟山模拟)在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是CC1上一点,且CF=2a.