题目内容
某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科目B的考试.已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书,现某人参加这项考试,科目A的正考和补考成绩合格的概率分别为 、
、 ,科目B的正考和补考成绩合格的概率均为
,科目B的正考和补考成绩合格的概率均为 ,假设各次考试成绩合格与否均互不影响.
,假设各次考试成绩合格与否均互不影响.
(1)求他不需要补考就可获得证书的概率;
(2)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为ξ,求ξ的分布列和数学期望.
解:(1)记“他不需要补考就可获得证书”为事件A,则P(A)= =
= ;
;
(2)ξ的可能取值为:2,3,4,则
P(ξ=2)=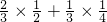 =
= ;P(ξ=3)=
;P(ξ=3)=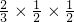 +
+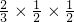 +
+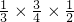 =
=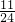 ;
;
P(ξ=4)=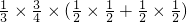 =
=
∴ξ的分布列为
Eξ=2× +3×
+3×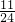 +4×
+4× =
=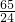
分析:(1)不需要补考就获得证书的事件表示科目A第一次考试合格且科目B第一次考试合格,这两次考试合格是相互独立的,根据相互独立事件同时发生的概率,得到结果;
(2)参加考试的次数为ξ,由已知得,ξ=2,3,4,注意到各事件之间的独立性与互斥性,根据相互独立事件同时发生的概率写出概率,即可求出ξ的分布列和数学期望.
点评:本题考查离散型随机变量的分布列和期望,考查相互独立事件同时发生的概率,考查学生的计算能力,属于中档题.
 =
= ;
;(2)ξ的可能取值为:2,3,4,则
P(ξ=2)=
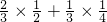 =
= ;P(ξ=3)=
;P(ξ=3)=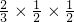 +
+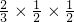 +
+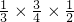 =
=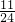 ;
;P(ξ=4)=
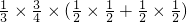 =
=
∴ξ的分布列为
| P | 2 | 3 | 4 |
| ξ |  | 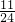 |  |
 +3×
+3×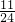 +4×
+4× =
=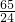
分析:(1)不需要补考就获得证书的事件表示科目A第一次考试合格且科目B第一次考试合格,这两次考试合格是相互独立的,根据相互独立事件同时发生的概率,得到结果;
(2)参加考试的次数为ξ,由已知得,ξ=2,3,4,注意到各事件之间的独立性与互斥性,根据相互独立事件同时发生的概率写出概率,即可求出ξ的分布列和数学期望.
点评:本题考查离散型随机变量的分布列和期望,考查相互独立事件同时发生的概率,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
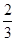 ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为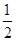 ,假设各次考试成绩合格与否均互不影响。
,假设各次考试成绩合格与否均互不影响。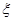 ,求
,求