题目内容
已知
,设命题
函数
在R上单调递减，
不等式
的解集为R,若
和
中有且只有一个命题为真命题，求
的取值范围.
【答案】
解
由函数
在R上单调递减知
，所以命题
为真命题时
的取值范围是,
令
, 则
不等式
的解集为R，
只要
即可，而函数
在R上的最小值为
，
所以
，即
即
真
若真假,则
若假真，则
,
所以命题和有且只有一个命题正确时的取值范围是
或.
【解析】略
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
,设命题
函数
在R上单调递减，
不等式
的解集为R,若
和
中有且只有一个命题为真命题，求
的取值范围.
，设命题
函数
在R上单调递增；命题
不等式
对任意
恒成立。若
且
为假，
的取值范围。
,设命题
函数
在R上单调递减，
不等式
的解集为R,若
和
中有且只有一个命题为真命题，求
的取值范围.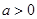
，设p:函数
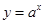在R上单调递减；命题q:方程
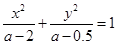表示的曲线是双曲线，如果“p
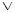q”为真，“p
q”为假，求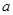
的取值范围.