题目内容
下列函数中，既是偶函数又在(0，＋∞)单调递增的函数是( )．
| A．y＝x3 | B．y＝|x|＋1 |
C． | D．y＝2－|x| |
B
解析试题分析：由f(-x)=f(x)可知B，C，D为偶函数，但又因为函数在在(0，＋∞)单调递增,所以应选B.
考点：函数的奇偶性和单调性.
点评：若函数的定义域关于原点对称，则f(-x)=f(x)为偶函数，f(-x)=-f(x)是奇函数，然后再结合图像判断单调性，是解此类小题的一般规律.
练习册系列答案
相关题目
的图象可能是 （ ）
函数
在下列哪个区间内有零点
A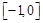． | B． | C． | D． |
（其中
），在同一坐标系中画出其中的两个函数在第一象限内的图像，其中正确的是（ ）
定义在
上的偶函数
满足
，且
，则
的值为（ ）
A． | B． | C． | D． |
已知函数
定义域是
，则
的定义域是（ ）
A． | B． | C． | D． |
定义在
上的函数
，则
的图像与直线
的交点为
、
、
且
，则下列说法错误的是（ ）
A． | B． |
C． | D． |
的定义域为R，且定义如下：
（其中M是实数集R的非空真子集），在实数集R上有两个非空真子集A、B满足
，则函数
的值域为 （ ）
下列函数中，与函数
是同一函数的是（ ）
A． | B． | C． | D． |