题目内容
函数 是( )
是( )
A.奇函数且在 上单调递增 上单调递增 | B.奇函数且在 上单调递增 上单调递增 |
C.偶函数且在 上单调递增 上单调递增 | D.偶函数且在 上单调递增 上单调递增 |
C
解析试题分析:因为】函数 =-cos2x,那么可知余弦函数为偶函数,则可知cos2x=y为偶函数,排除A,B,另外将余弦函数的性质来分析可知
=-cos2x,那么可知余弦函数为偶函数,则可知cos2x=y为偶函数,排除A,B,另外将余弦函数的性质来分析可知 得到的区间为递增区间,故可知答案为C.
得到的区间为递增区间,故可知答案为C.
考点:三角函数的性质
点评:主要是二倍角公式的化简和性质的运用,属于基础题。

练习册系列答案
相关题目
已知 ,则
,则
A. | B. |
C. | D. |
如图,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针尖位置p(x,y).若初始位置为P0( ,
, ),当秒针从P0(注:此时t=0)正常开始走时,那么点P的纵坐标y与时间t的函数关系为( )
),当秒针从P0(注:此时t=0)正常开始走时,那么点P的纵坐标y与时间t的函数关系为( )
A. |
B. |
C. |
D. |
下列各式中,值为 的是( )
的是( )
A. | B. |
C. | D. |
 ( )
( )
A. | B. | C.- | D.- |
为了得到函数 的图象,可将函数
的图象,可将函数 的图象( )
的图象( )
A.向左平移 个长度单位 个长度单位 | B.向左平移 个长度单位 个长度单位 |
C.向右平移 个长度单位 个长度单位 | D.向右平移 个长度单位 个长度单位 |
要得到函数 的导函数
的导函数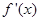 的图象,只需将
的图象,只需将 的图象( )
的图象( )
A.向左平移 个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) 个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) |
B.向左平移 个单位,再把各点的纵坐标缩短到原来的 个单位,再把各点的纵坐标缩短到原来的 倍(横坐标不变) 倍(横坐标不变) |
C.向左平移 个单位,再把各点的纵坐标伸长到原来的 个单位,再把各点的纵坐标伸长到原来的 倍(横坐标不变) 倍(横坐标不变) |
D.向左平移 个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) 个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) |
为了得到函数 的图象,可以将函数
的图象,可以将函数 的图象( )
的图象( )
A.向右平移 个长度单位 个长度单位 | B.向左平移 个长度单位 个长度单位 |
C.向右平移 个长度单位 个长度单位 | D.向左平移 个长度单位 个长度单位 |
函数 ,
, 的单调递减区间是
的单调递减区间是
A. | B. | C. | D. |