题目内容
已知抛物线y2=2px(p>0)的焦点F与椭圆 的一个焦点重合,它们在第一象限内的交点为T,且TF与x轴垂直,则椭圆的离心率为________.
的一个焦点重合,它们在第一象限内的交点为T,且TF与x轴垂直,则椭圆的离心率为________.

分析:由条件可得b2=2ac,再根据c2 +b2 -a2=0,即c2+2ac-a2=0,两边同时除以a2,化为关于
 的一元二次方程,解方程求出椭圆的离心率
的一元二次方程,解方程求出椭圆的离心率 的值.
的值.解答:依题意
 ,∴b2=2ac,
,∴b2=2ac,又c2 +b2 -a2=0,∴c2+2ac-a2=0,∴e2+2e-1=0,
解得
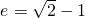 .
.故答案为
 -1.
-1.点评:本题考查抛物线与椭圆的简单性质,以及一元二次方程的解法.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目