题目内容

【题目】定义在[﹣1，1]的函数f（x）满足下列两个条件：①任意的x∈[﹣1，1]，都有f（﹣x）=﹣f（x）；②任意的m，n∈[0，1]，当m≠n，都有 ＜0，则不等式f（1﹣3x）＜f（x﹣1）的解集是（ ）
A.[0， ）
B.（ ， ]
C.[﹣1， ）
D.[ ，1]

【答案】A
【解析】解：∵任意的x∈[﹣1，1]，都有f（﹣x）=﹣f（x），
∴f（0）=0，f（x）是[﹣1，1]上的奇函数，
∵任意的m，n∈[0，1]，当m≠n，都有 ＜0，
∴f（x）在[0，1]上是递减函数，
∴f（x）在[﹣1，0]上也是递减函数，
即f（x）在[﹣1，1]上是递减函数，
∴不等式f（1﹣3x）＜f（x﹣1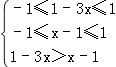） 即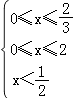
∴0≤x ，
故解集为[0， ）．
故选：A．

练习册系列答案
相关题目

【题目】已知函数f（x）=x|x﹣a|+2x．
（1）若函数f（x）在R上是增函数，求实数a的取值范围；
（2）求所有的实数a，使得对任意x∈[1，2]时，函数f（x）的图象恒在函数g（x）=2x+1图象的下方；
（3）若存在a∈[﹣4，4]，使得关于x的方程f（x）=tf（a）有三个不相等的实数根，求实数t的取值范围．

【题目】设m是实数，f（x）=m﹣ （x∈R）
（1）若函数f（x）为奇函数，求m的值；
（2）试用定义证明：对于任意m，f（x）在R上为单调递增函数；
（3）若函数f（x）为奇函数，且不等式f（k3x）+f（3x﹣9x﹣2）＜0对任意x∈R恒成立，求实数k的取值范围．

【题目】已知函数f（x）是一次函数，g（x）是反比例函数，且满足f[f（x）]=x+2，g（1）=﹣1
（1）求函数f（x）和g（x）；
（2）设h（x）=f（x）+g（x），判断函数h（x）在（0，+∞）上的单调性，并用定义加以证明．

【题目】偶函数y=f（x）在区间[﹣4，0]上单调递增，则有（ ）
A.f（﹣1）＞f（ ）＞f（﹣π）
B.f（ ）＞f（﹣1）＞f（﹣π）
C.f（﹣π）＞f（﹣1）＞f（ ）
D.f（﹣1）＞f（﹣π）＞f（ ）

【题目】已知复数z=（2m2+3m﹣2）+（m2+m﹣2）i，（m∈R）根据下列条件，求m值．
（1）z是实数；
（2）z是虚数；
（3）z是纯虚数；
（4）z=0．

【题目】某学校拟建一块周长为400m的操场如图所示，操场的两头是半圆形，中间区域是矩形，学生做操一般安排在矩形区域，为了能让学生的做操区域尽可能大，试问如何设计矩形的长和宽？

【题目】设函数f（x）=ax2－lnx。

（Ⅰ）当a=时，判断f（x）的单调性；（Ⅱ）设f（x）≤x3+4x－lnx，在定义域内恒成立，求a的取值范围。

【题目】对于函数f（x）定义域中任意的x1 ， x2（x1≠x2）有如下结论
1）f（x1+x2）=f（x1）f（x2）
2）f（x1x2）=f（x1）+f（x2）
3） ＞0
4）f（ ）＜
5）f（ ）＞
6）f（﹣x）=f（x）．
当f（x）=lgx时，上述结论正确的序号为 ． （注：把你认为正确的命题的序号都填上）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网