题目内容
设函数f(x)=x2-(a-2)x-alnx.
(1)求函数f(x)的单调区间;
(2)若函数有两个零点,求满足条件的最小正整数a的值;
(3)若方程f(x)=c有两个不相等的实数根x1,x2,求证: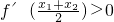 .
.
解:(1)x∈(0,+∞).
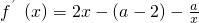 =
= =
=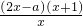 .
.
当a≤0时,f′(x)>0,函数f(x)在(0,+∞0上单调递增,即f(x)的单调递增区间为(0,+∞).
当a>0时,由f′(x)>0得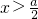 ;由f′(x)<0,解得
;由f′(x)<0,解得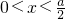 .
.
所以函数f(x)的单调递增区间为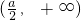 ,单调递减区间为
,单调递减区间为 .
.
(2)由(1)可得,若函数f(x)有两个零点,则a>0,且f(x)的最小值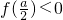 ,即
,即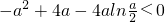 .
.
∵a>0,∴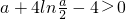 .
.
令h(a)=a+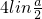 -4,可知h(a)在(0,+∞)上为增函数,且h(2)=-2,h(3)=
-4,可知h(a)在(0,+∞)上为增函数,且h(2)=-2,h(3)=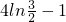 =
= ,
,
所以存在零点h(a0)=0,a0∈(2,3),
当a>a0时,h(a)>0;当0<a<a0时,h(a)<0.
所以满足条件的最小正整数a=3.
又当a=3时,f(3)=3(2-ln3)>0,f(1)=0,∴a=3时,f(x)由两个零点.
综上所述,满足条件的最小正整数a的值为3.
(3)∵x1,x2是方程f(x)=c得两个不等实数根,由(1)可知:a>0.
不妨设0<x1<x2.则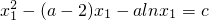 ,
, .
.
两式相减得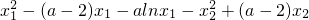 +alnx2=0,
+alnx2=0,
化为a=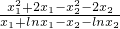 .
.
∵ ,当
,当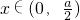 时,f′(x)<0,当
时,f′(x)<0,当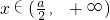 时,f′(x)>0.
时,f′(x)>0.
故只要证明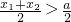 即可,
即可,
即证明x1+x2>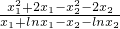 ,即证明
,即证明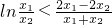 ,
,
设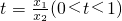 ,令g(t)=lnt-
,令g(t)=lnt-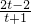 ,则
,则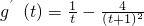 =
= .
.
∵1>t>0,∴g′(t)>0
.∴g(t)在(0,1)上是增函数,又在t=1处连续且g(1)=0,
∴当t∈(0,1)时,g(t)<0纵成立.故命题得证.
分析:(1)对a分类讨论,利用导数与函数单调性的关系即可得出;
(2)由(1)可得,若函数f(x)有两个零点,则a>0,且f(x)的最小值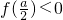 ,即
,即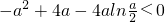 .可化为h(a)=
.可化为h(a)=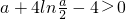 .利用单调性判断其零点所处的最小区间即可得出;
.利用单调性判断其零点所处的最小区间即可得出;
(3))由x1,x2是方程f(x)=c得两个不等实数根,由(1)可知:a>0.不妨设0<x1<x2.则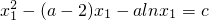 ,
, .
.
两式相减得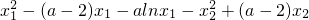 +alnx2=0,化为a=
+alnx2=0,化为a=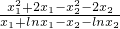 .由
.由 ,当
,当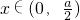 时,f′(x)<0,当
时,f′(x)<0,当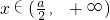 时,f′(x)>0.故只要证明
时,f′(x)>0.故只要证明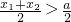 即可,即证明
即可,即证明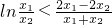 ,令
,令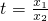 换元,再利用导数即可证明.
换元,再利用导数即可证明.
点评:本题综合考查了利用导数研究函数的单调性、极值与最值等基础知识,及其分类讨论思想方法、等价转化方法、换元法等基本技能与方法.
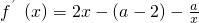 =
= =
=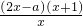 .
.当a≤0时,f′(x)>0,函数f(x)在(0,+∞0上单调递增,即f(x)的单调递增区间为(0,+∞).
当a>0时,由f′(x)>0得
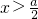 ;由f′(x)<0,解得
;由f′(x)<0,解得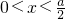 .
.所以函数f(x)的单调递增区间为
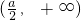 ,单调递减区间为
,单调递减区间为 .
.(2)由(1)可得,若函数f(x)有两个零点,则a>0,且f(x)的最小值
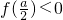 ,即
,即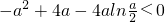 .
.∵a>0,∴
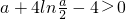 .
.令h(a)=a+
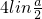 -4,可知h(a)在(0,+∞)上为增函数,且h(2)=-2,h(3)=
-4,可知h(a)在(0,+∞)上为增函数,且h(2)=-2,h(3)=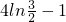 =
= ,
,所以存在零点h(a0)=0,a0∈(2,3),
当a>a0时,h(a)>0;当0<a<a0时,h(a)<0.
所以满足条件的最小正整数a=3.
又当a=3时,f(3)=3(2-ln3)>0,f(1)=0,∴a=3时,f(x)由两个零点.
综上所述,满足条件的最小正整数a的值为3.
(3)∵x1,x2是方程f(x)=c得两个不等实数根,由(1)可知:a>0.
不妨设0<x1<x2.则
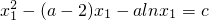 ,
, .
.两式相减得
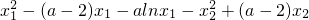 +alnx2=0,
+alnx2=0,化为a=
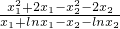 .
.∵
 ,当
,当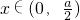 时,f′(x)<0,当
时,f′(x)<0,当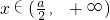 时,f′(x)>0.
时,f′(x)>0.故只要证明
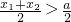 即可,
即可,即证明x1+x2>
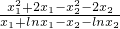 ,即证明
,即证明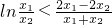 ,
,设
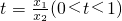 ,令g(t)=lnt-
,令g(t)=lnt-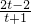 ,则
,则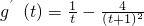 =
= .
.∵1>t>0,∴g′(t)>0
.∴g(t)在(0,1)上是增函数,又在t=1处连续且g(1)=0,
∴当t∈(0,1)时,g(t)<0纵成立.故命题得证.
分析:(1)对a分类讨论,利用导数与函数单调性的关系即可得出;
(2)由(1)可得,若函数f(x)有两个零点,则a>0,且f(x)的最小值
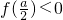 ,即
,即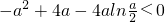 .可化为h(a)=
.可化为h(a)=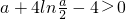 .利用单调性判断其零点所处的最小区间即可得出;
.利用单调性判断其零点所处的最小区间即可得出;(3))由x1,x2是方程f(x)=c得两个不等实数根,由(1)可知:a>0.不妨设0<x1<x2.则
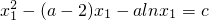 ,
, .
.两式相减得
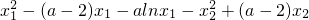 +alnx2=0,化为a=
+alnx2=0,化为a=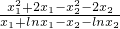 .由
.由 ,当
,当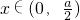 时,f′(x)<0,当
时,f′(x)<0,当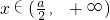 时,f′(x)>0.故只要证明
时,f′(x)>0.故只要证明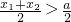 即可,即证明
即可,即证明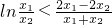 ,令
,令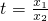 换元,再利用导数即可证明.
换元,再利用导数即可证明.点评:本题综合考查了利用导数研究函数的单调性、极值与最值等基础知识,及其分类讨论思想方法、等价转化方法、换元法等基本技能与方法.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目