题目内容
已知椭圆C: +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为
,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为 .
.

(1)求椭圆C的方程;
(2)过原点且斜率为 的直线l,与椭圆交于E,F点,试判断∠EF2F是锐角、直角还是钝角,并写出理由;
的直线l,与椭圆交于E,F点,试判断∠EF2F是锐角、直角还是钝角,并写出理由;
(3)P是椭圆上异于A1,A2的任一点,直线PA1,PA2,分别交 轴于点N,M,若直线OT与过点M,N 的圆G相切,切点为T.证明:线段OT的长为定值,并求出该定值.
轴于点N,M,若直线OT与过点M,N 的圆G相切,切点为T.证明:线段OT的长为定值,并求出该定值.
(1)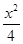 +y2=1 ;(2) ∠EF2F是锐角;(3) 线段OT的长度为定值2.
+y2=1 ;(2) ∠EF2F是锐角;(3) 线段OT的长度为定值2.
【解析】
试题分析:(1)因为椭圆C的离心率e=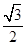 ,故设a=2m,c=
,故设a=2m,c=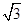 m,则b=m,直线A2B2方程为
bx ay ab=0,所以
m,则b=m,直线A2B2方程为
bx ay ab=0,所以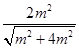 =
=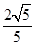 ,解得m=1,故椭圆方程为
,解得m=1,故椭圆方程为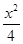 +y2=1; (2)联立椭圆和直线方程解出交点坐标E(
+y2=1; (2)联立椭圆和直线方程解出交点坐标E(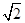 ,
,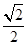 ),F(
),F( 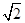 ,
,
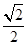 ) ,根据向量数量积为正可判断∠EF2F是锐角;(3) 由(1)可知A1(0,1)A2(0,1),设P(x0,y0),
直线PA1:y 1=
) ,根据向量数量积为正可判断∠EF2F是锐角;(3) 由(1)可知A1(0,1)A2(0,1),设P(x0,y0),
直线PA1:y 1=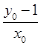 x,令y=0,得xN=
x,令y=0,得xN=
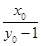 ,直线PA2:y+1=
,直线PA2:y+1=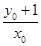 x,令y=0,得xM=
x,令y=0,得xM=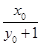 ,接下来有两种方法,解法一,设圆G的圆心为(
,接下来有两种方法,解法一,设圆G的圆心为(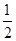 (
(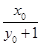
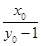 ),h),利用圆的方程和勾股定理求解;解法二,OM·ON=|(
),h),利用圆的方程和勾股定理求解;解法二,OM·ON=|( 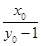 )·
)·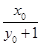 |=
|=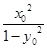 ,利用切割线定理得求解.
,利用切割线定理得求解.
试题解析:(1)因为椭圆C的离心率e=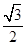 ,
,
故设a=2m,c=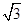 m,则b=m.
m,则b=m.
直线A2B2方程为 bx ay ab=0,
即mx 2my 2m2=0.
所以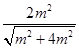 =
=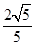 ,解得m=1.
,解得m=1.
所以 a=2,b=1,椭圆方程为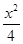 +y2=1.
5分
+y2=1.
5分
由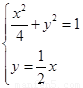 得E(
得E(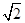 ,
,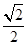 ),F(
),F( 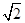 ,
,
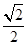 ).
.7分
).
.7分
又F2(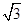 ,0),所以
,0),所以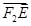 =(
=(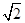
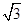 ,
,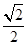 ),
),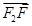 =(
=( 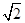
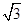 ,
,
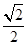 ),
),
所以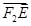 ·
·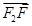 =(
=(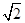
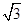 )×(
)×( 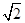
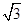 )+
)+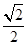 ×(
×( 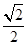 )=
)=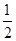 >0.
>0.
所以∠EF2F是锐角. 10分
(3)由(1)可知A1(0,1) A2(0, 1),设P(x0,y0),
直线PA1:y 1=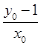 x,令y=0,得xN=
x,令y=0,得xN=
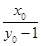 ;
;
直线PA2:y+1=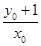 x,令y=0,得xM=
x,令y=0,得xM=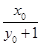 ;
12分
;
12分
解法一:设圆G的圆心为(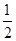 (
(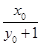
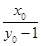 ),h),
),h),
则r2=[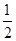 (
(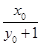
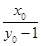 )
)
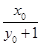 ]2+h2=
]2+h2=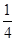 (
(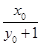 +
+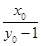 )2+h2.
)2+h2.
OG2=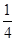 (
(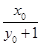
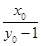 )2+h2.
)2+h2.
OT2=OG2
r2=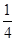 (
(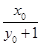
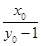 )2+h2
)2+h2 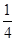 (
(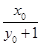 +
+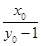 )2 h2=
)2 h2=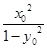 . .14分
. .14分
而 +y02=1,所以x02=4(1 y02),所以OT2=4,
+y02=1,所以x02=4(1 y02),所以OT2=4,
所以OT=2,即线段OT的长度为定值2. 16分
解法二:OM·ON=|( 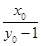 )·
)·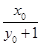 |=
|=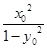 ,
,
而 +y02=1,所以x02=4(1 y02),所以OM·ON=4.
+y02=1,所以x02=4(1 y02),所以OM·ON=4.
由切割线定理得OT2=OM·ON=4.
所以OT=2,即线段OT的长度为定值2. 16分
考点:椭圆直线综合、点到直线距离公式、向量数量积的计算、圆的方程.

 快捷英语周周练系列答案
快捷英语周周练系列答案 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l的距离为
,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l的距离为 .
. =
= +
+ 成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.
成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.