题目内容
设数列{an}的前项和为Sn,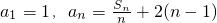 .
.
(1)求数列{an}的通项an的表达式;
(2)是否存在自然数n,使得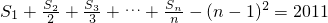 ?若存在,求出n的值;若不存在,请说明理由.
?若存在,求出n的值;若不存在,请说明理由.
解:(1)∵ ,
,
∴nan=sn+2n(n-1)①,
(n-1)an-1=sn-1+2(n-1)(n-2)(n≥2)②,
①-②有:(n-1)an-(n-1)an-1=4(n-1)(n≥2),
∴an-an-1=4(n≥2),
∴{an}是1为首项,4为公差的等差数列,
∴an=4n-3.
(2)由已知条件可得,当n≥2时, ,
,
整理得:(n-1)sn-nsn-1=2n(n-1),等式两端同除以n(n-1),
得 (n≥2),又
(n≥2),又 ,
,
∴ 是1为首项,2为公差的等差数列,
是1为首项,2为公差的等差数列,
∴ .
.
∴ =
= =2n-1,
=2n-1,
∴存在自然数n,使等式成立,则2n-1=2011,解得n=1006,合乎题意.
分析:(1)已知sn求an是数列中的常见题形,解决的办法是分n=1与n≥2两种情况分别求得a1与an,从而可求得an;
(2)在n≥2时,an=sn-sn-1= ,经过合理转化,可得
,经过合理转化,可得 ,又a1=1,利用等差数列的定义可以求得
,又a1=1,利用等差数列的定义可以求得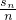 ,从而问题解决.
,从而问题解决.
点评:本题考查递推数列,考查数列通项公式的求法与数列求和,解题的关键是合理转化,利用等差数列的定义求通项,利用等差数列的求和公式求数列的和.
 ,
,∴nan=sn+2n(n-1)①,
(n-1)an-1=sn-1+2(n-1)(n-2)(n≥2)②,
①-②有:(n-1)an-(n-1)an-1=4(n-1)(n≥2),
∴an-an-1=4(n≥2),
∴{an}是1为首项,4为公差的等差数列,
∴an=4n-3.
(2)由已知条件可得,当n≥2时,
 ,
,整理得:(n-1)sn-nsn-1=2n(n-1),等式两端同除以n(n-1),
得
 (n≥2),又
(n≥2),又 ,
,∴
 是1为首项,2为公差的等差数列,
是1为首项,2为公差的等差数列,∴
 .
.∴
 =
= =2n-1,
=2n-1,∴存在自然数n,使等式成立,则2n-1=2011,解得n=1006,合乎题意.
分析:(1)已知sn求an是数列中的常见题形,解决的办法是分n=1与n≥2两种情况分别求得a1与an,从而可求得an;
(2)在n≥2时,an=sn-sn-1=
 ,经过合理转化,可得
,经过合理转化,可得 ,又a1=1,利用等差数列的定义可以求得
,又a1=1,利用等差数列的定义可以求得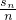 ,从而问题解决.
,从而问题解决.点评:本题考查递推数列,考查数列通项公式的求法与数列求和,解题的关键是合理转化,利用等差数列的定义求通项,利用等差数列的求和公式求数列的和.

练习册系列答案
相关题目
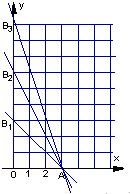 在平面直角坐标系上,设不等式组
在平面直角坐标系上,设不等式组