题目内容
已知圆x2+y2+x-6y+m=0和直线x+2y-3=0交于P,Q两点,且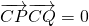 ( C为圆心).则该圆的半径为________,m的值为________.
( C为圆心).则该圆的半径为________,m的值为________.


分析:把圆的方程化为标准方程,找出圆心C的坐标,表示出圆C的半径r,然后由点到直线的距离公式求出圆心到已知直线的距离d,由
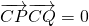 得到CP⊥CQ,即三角形CPQ为等腰直角三角形,根据余弦函数定义得到d=CPcos45°,求出CP的长,即为圆C的半径,然后用求出的圆的半径等于表示出的半径r,列出关于m的方程,求出方程的解得到m的值.
得到CP⊥CQ,即三角形CPQ为等腰直角三角形,根据余弦函数定义得到d=CPcos45°,求出CP的长,即为圆C的半径,然后用求出的圆的半径等于表示出的半径r,列出关于m的方程,求出方程的解得到m的值.解答:把圆x2+y2+x-6y+m=0化为标准方程得:(x+
 )2+(y-3)2=
)2+(y-3)2=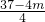 ,
,∴圆心
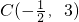 ,半径
,半径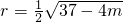 ,
,则圆心
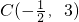 圆心到直线x+2y-3=0的距离d=
圆心到直线x+2y-3=0的距离d=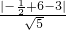 =
= .
.又∵
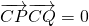 ,
,∴CP⊥CQ,又CP=CQ,
∴△CPQ为等腰直角三角形,
∴CP=
 d=
d= ,即圆C的半径为
,即圆C的半径为 ,
,由
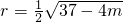 =
= ,解得:
,解得: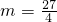 .
.故答案为:
 ;
;
点评:此题考查了直线与圆相交的性质,点到直线的距离公式,以及平面向量的数量积的运算,由平面向量的数量积为0得到两向量互相垂直是解本题的突破点,同时要求学生会将圆的一般式方程化为标准方程,会从圆的标准方程中找出圆心坐标和圆的半径.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目