题目内容
![]() .
.
(1)若![]() 求
求![]() 的单调区间及
的单调区间及![]() 的最小值;
的最小值;
(2)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(3)试比较![]() 与
与![]() 的大小.
的大小.![]() ,并证明你的结论.
,并证明你的结论.
(1)![]()
当![]() 时,
时,![]()
![]() 在区间
在区间![]() 上是递增的. …………2分
上是递增的. …………2分
当![]() 时,
时,![]()
![]() 在区间
在区间![]() 上是递减的.
上是递减的.
故![]() 时,
时,![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ,
,![]() .…………4分
.…………4分
(2)若![]() ,当
,当![]() 时,
时,![]()
![]()
则![]() 在区间
在区间![]() 上是递增的;
上是递增的;
当![]() 时,
时,![]() ,
, ![]()
![]() 在区间
在区间![]() 上是递减的. …………6分
上是递减的. …………6分
若![]() ,当
,当![]() 时,
时,![]()
![]()
则![]() 在区间
在区间![]() 上是递增的,
上是递增的, ![]() 在区间
在区间![]() 上是递减的;
上是递减的;
当![]() 时,
时,![]() ,
, ![]()
![]() 在区间
在区间![]() 上是递减的,而
上是递减的,而![]() 在
在![]() 处有意义;
处有意义;
则![]() 在区间
在区间![]() 上是递增的,在区间
上是递增的,在区间![]() 上是递减的. …………8分
上是递减的. …………8分
综上: 当![]() 时,
时, ![]() 的递增区间是
的递增区间是![]() ,递减区间是
,递减区间是![]() ;
;
当![]() ,
,![]() 的递增区间是
的递增区间是![]() ,递减区间是
,递减区间是![]() . …………9分
. …………9分
(3)由(1)可知,当![]() 时,有
时,有![]() 即
即![]()
![]()
![]()
=![]() . …………14分
. …………14分

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 .
. 的单调区间与极值;
的单调区间与极值; ,使得对任意的
,使得对任意的 ,当
,当 时恒有
时恒有 成立.若存在,求
成立.若存在,求 是自然对数的底)
是自然对数的底) 的单调区间;
的单调区间; 时,若方程
时,若方程 在区间
在区间 上有两个不同的实根,求证:
上有两个不同的实根,求证: 。
。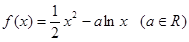
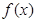 的单调区间;
的单调区间;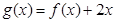 ,若
,若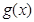 在
在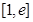 上不单调且仅在
上不单调且仅在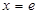 处取得最大值,求
处取得最大值,求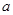 的取值范围.
的取值范围.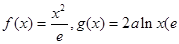 为自然对数的底数)
为自然对数的底数)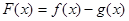 的单调区间,若
的单调区间,若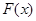 有最值,请求出最值;
有最值,请求出最值;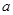 ,使
,使 的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出
的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出